题目内容
1.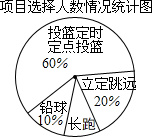 某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.
某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.训练后篮球定点投篮测试进球统计表
| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
(1)训练后篮球定时定点投篮人均进球数为5个;
(2)选择长跑训练的人数占全班人数的百分比是10%,该班共有同学40人;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
分析 (1)根据平均数的概念计算平均进球数;
(2)根据所有人数的比例和为1计算选择长跑训练的人数占全班人数的百分比;由总人数=某种运动的人数÷所占比例计算总人数;
(3)通过比较训练前后的成绩,利用增长率的意义即可列方程求解.
解答 解:(1)参加篮球训练的人数是:2+1+4+7+8+2=24(人).
训练后篮球定时定点投篮人均进球数=$\frac{8×2+7×1+6×4+5×7+4×8+3×2}{24}$=5(个).
故答案是:5;
(2)由扇形图可以看出:选择长跑训练的人数占全班人数的百分比=1-60%-10%-20%=10%,
则全班同学的人数为24÷60%=40(人),
故答案是:10%,40;
(3)设参加训练之前的人均进球数为x个,
则x(1+25%)=5,解得 x=4.
即参加训练之前的人均进球数是4个.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
12.若点P1(x1,y1),P2(x2,y2)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,且x1=-x2,则( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | y1=-y2 |
9.今年来某县加大了对教育经费的投入,2013年投入2500万元,2015年投入3500万元.假设该县投入教育经费的年平均增长率为x,根据题意列方程,则下列方程正确的是( )
| A. | 2500x2=3500 | B. | 2500(1+x)2=3500 | ||
| C. | 2500(1+x%)2=3500 | D. | 2500(1+x)+2500(1+x)2=3500 |
6. 如图所示几何体的左视图是( )
如图所示几何体的左视图是( )
 如图所示几何体的左视图是( )
如图所示几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
13.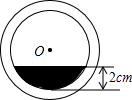 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )| A. | ($\frac{16}{3}$π-4$\sqrt{3}$)cm2 | B. | ($\frac{16}{3}$π-8$\sqrt{3}$)cm2 | C. | ($\frac{8}{3}$π-4$\sqrt{3}$)cm2 | D. | ($\frac{4}{3}$π-2$\sqrt{3}$)cm2 |
