题目内容
8.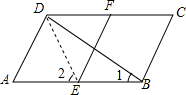 已知如图所示,在?ABCD中,∠A=60°,E,F分别是AB,CD中点,AB=2AD.求证:BD=$\sqrt{3}$EF.
已知如图所示,在?ABCD中,∠A=60°,E,F分别是AB,CD中点,AB=2AD.求证:BD=$\sqrt{3}$EF.
分析 先连接,DE构造平行四边形,再利用平行四边形及等边三角形的性质解答.
解答 证明:连结DE,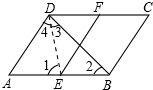
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵DF=$\frac{1}{2}$CD,AE=$\frac{1}{2}$AB,
∴DF=AE,DF∥AE,
∴四边形ADFE是平行四边形.
∴EF=AD,
∴AB=2AE,
∴AD=AE.
∴∠1=∠4.
∵∠A=60°,∠1+∠4+∠A=180°,
∴∠1=∠A=∠4=60°.
∴△ADE是等边三角形,
∴DE=AE.
∵AE=BE,
∴DE=BE,
∴∠2=∠3.
∵∠1=∠2+∠3,∠1=60°,
∴∠2=∠3=30°.
∴∠ADB=∠3+∠4=90°
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}=\sqrt{(2AD)^{2}-A{D}^{2}}=\sqrt{3}AD$,
∴BD=$\sqrt{3}$EF.
点评 本题考查了平行四边形的性质和判定,解答此题的关键是构造平行四边形,用平行四边形及等边三角形的性质,直角三角形的性质解答.

练习册系列答案
相关题目
3. 如图所示,已知直线a与b相交,直线c与d平行,则图中内错角共有( )
如图所示,已知直线a与b相交,直线c与d平行,则图中内错角共有( )
 如图所示,已知直线a与b相交,直线c与d平行,则图中内错角共有( )
如图所示,已知直线a与b相交,直线c与d平行,则图中内错角共有( )| A. | 48对 | B. | 24对 | C. | 16对 | D. | 8对 |
20.设4-$\sqrt{2}$的整数部分为a,小数部分为b,则a-$\frac{1}{b-2}$的值为( )
| A. | 2+$\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2-$\frac{\sqrt{2}}{2}$ | D. | -$\sqrt{2}$ |
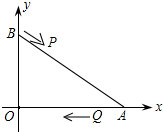 如图,A、B两点的坐标分别是(8,0)、(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t秒(0<t<$\frac{10}{4}$).解答如下问题:
如图,A、B两点的坐标分别是(8,0)、(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t秒(0<t<$\frac{10}{4}$).解答如下问题: 如图所示,⊙O的弦AB、CD交于点P,连接AC、BD,求证:△BDP∽△CAP.
如图所示,⊙O的弦AB、CD交于点P,连接AC、BD,求证:△BDP∽△CAP. 如图,A,B两港间距离为74km,一轮船从离A港10km的P地出发向B港匀速行驶,30min后离A港26km(未到达B港),设出发xh后,轮船离A港ykm(未到达B港).
如图,A,B两港间距离为74km,一轮船从离A港10km的P地出发向B港匀速行驶,30min后离A港26km(未到达B港),设出发xh后,轮船离A港ykm(未到达B港).