题目内容
9.化简:$\frac{\sqrt{2}(\sqrt{6}-\sqrt{3}-\sqrt{2}+\sqrt{1})}{\sqrt{3-2\sqrt{2}}•{\sqrt{2-\sqrt{3}}}$.分析 先把分母的复合二次根式化简,再把分子部分利用因式分解的方法分解,然后约分即可.
解答 解:原式=$\frac{\sqrt{2}(\sqrt{6}-\sqrt{3}-\sqrt{2}+1)}{\sqrt{(\sqrt{2}-1)^{2}}•\sqrt{\frac{(\sqrt{3}-1)^{2}}{2}}}$
=$\frac{2[\sqrt{3}(\sqrt{2}-1)-(\sqrt{2}-1)]}{(\sqrt{2}-1)(\sqrt{3}-1)}$
=$\frac{2(\sqrt{2}-1)(\sqrt{3}-1)}{(\sqrt{2}-1)(\sqrt{3}-1)}$
=2.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
相关题目
17.若不等式x-1<a的正整数解是1,2,3,则a的取值范围是( )
| A. | 2<a<3 | B. | 3<a≤4 | C. | 2<a≤3 | D. | 2≤a≤3 |
4.如图1,在矩形ABCD中,AB=2,动点P从点B出发,沿路线B→C→D作匀速运动,图2是此运动过程中,△PAB的面积S与点P运动的路程x之间的函数图象的一部分,则BC的长为( )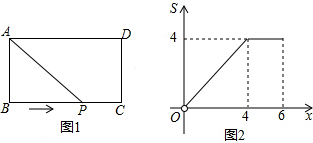

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
14.下列各组x、y的值,是二元一次方程x-y=5的一个解的是( )
| A. | $\left\{\begin{array}{l}x=-1\\ y=-4\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=1\\ y=-4\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-1\\ y=4\end{array}\right.$ |
18.下列说法中正确的是( )
| A. | 36的平方根是6 | B. | 8的立方根是2 | ||
| C. | $\sqrt{4}$的平方根是±2 | D. | 9的算术平方根是-3 |
19. 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )
 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )| A. | 0 | B. | -3×($\frac{2}{3}$$\sqrt{3}$)2015 | C. | (2$\sqrt{3}$)2016 | D. | 3×($\frac{2}{3}$$\sqrt{3}$)2015 |