题目内容
9.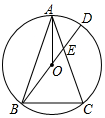 如图,△ABC中,AB=AC,⊙O为△ABC外接圆,BD为⊙O直径,DB交AC于E.连接AO
如图,△ABC中,AB=AC,⊙O为△ABC外接圆,BD为⊙O直径,DB交AC于E.连接AO(1)求证:AO⊥BC;
(2)若$\frac{BE}{DE}$=$\frac{7}{3}$,求$\frac{AE}{CE}$的值.
分析 (1)根据弦、弧、圆心角的关系得到$\widehat{AB}$=$\widehat{AC}$,根据垂径定理证明结论;
(2)连接DC,根据圆周角定理得到∠BCD=90°,得到AO∥DC,根据平行线分线段成比例定理计算即可.
解答 (1)证明:∵AB=AC,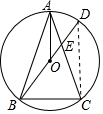
∴$\widehat{AB}$=$\widehat{AC}$,
∴AO⊥BC;
(2)解:连接DC,
∵$\frac{BE}{DE}$=$\frac{7}{3}$,
∴$\frac{OE}{ED}$=$\frac{2}{3}$,
∵BD为⊙O直径,
∴∠BCD=90°,又AO⊥BC,
∴AO∥DC,
∴$\frac{AE}{CE}$=$\frac{OE}{ED}$=$\frac{2}{3}$.
点评 本题考查的是三角形的外接圆和外心、垂径定理的应用、圆周角定理的应用,掌握垂径定理、直径所对的圆周角是直角、平行线分线段成比例定理是解题的关键.

练习册系列答案
相关题目
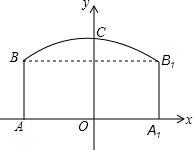 如图,隧道的截面由抛物线和长方形构成.长方形的长为12m,宽为5m,抛物线的最高点C离路面AA1的距离为8m,建立如图所示的直角坐标系.
如图,隧道的截面由抛物线和长方形构成.长方形的长为12m,宽为5m,抛物线的最高点C离路面AA1的距离为8m,建立如图所示的直角坐标系. 如图,在 11×16 的网格图中,△ABC 三个顶点坐标分别为 A(-4,0),B(-1,1),C(-2,3).
如图,在 11×16 的网格图中,△ABC 三个顶点坐标分别为 A(-4,0),B(-1,1),C(-2,3). 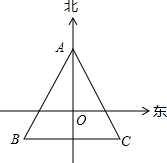 如图,等边△ABC的中心是点O,OA=3,请用OA的长与一个角度表示B、C两点的位置.
如图,等边△ABC的中心是点O,OA=3,请用OA的长与一个角度表示B、C两点的位置.