题目内容
8.点A(m-5,-2m)在第三象限,则m的取值范围是0<m<5.分析 根据第三象限内点的横坐标与纵坐标都是负数列出不等式组,然后求解即可.
解答 解:∵点A(m-5,-2m)在第三象限,
∴$\left\{\begin{array}{l}{m-5<0①}\\{-2m<0②}\end{array}\right.$,
解不等式①得,m<5,
解不等式②得,m>0,
所以,m的取值范围是0<m<5.
故答案为:0<m<5.
点评 本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知关于x的一元二次方程(k-2)2x2+(2k+1)x+1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>$\frac{4}{3}$且k≠2 | B. | k≥$\frac{4}{3}$且k≠2 | C. | k>$\frac{3}{4}$且k≠2 | D. | k≥$\frac{3}{4}$且k≠2 |
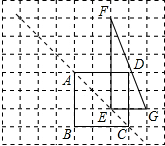 如图,方格纸中每个小正方形的边长均为1,正方形ABCD和△EFG的顶点都在小正方形的顶点上.
如图,方格纸中每个小正方形的边长均为1,正方形ABCD和△EFG的顶点都在小正方形的顶点上. 如图,已知AC、BD相交于点O,∠B=∠C=90°,且AB=4,OB=OD=3,CD=2,求AC的长.
如图,已知AC、BD相交于点O,∠B=∠C=90°,且AB=4,OB=OD=3,CD=2,求AC的长. 如图,已知直线上两点坐标,请求出这条直线的解析式,并判断点A(2,-6),B(3,-10),C(-2,5)是否坐此直线上?
如图,已知直线上两点坐标,请求出这条直线的解析式,并判断点A(2,-6),B(3,-10),C(-2,5)是否坐此直线上? 一天晚上,小伟帮妈妈清洗茶杯,三个茶杯只有花色不同,其中一个无盖(如图),在清洗过程中,突然停电了,小伟只好摸黑清洗
一天晚上,小伟帮妈妈清洗茶杯,三个茶杯只有花色不同,其中一个无盖(如图),在清洗过程中,突然停电了,小伟只好摸黑清洗