题目内容
2.不等式组$\left\{\begin{array}{l}{\frac{1}{2}(x+2)-2>0}\\{x>m}\end{array}\right.$的解集是x>4,那么m的取值范围是( )| A. | m≤4 | B. | m<4 | C. | m≥4 | D. | m>4 |
分析 首先解不等式$\frac{1}{2}$(x+2)-3>0得x>4,而x>m,并且不等式组解集为x>4,由此即可确定m的取值范围.
解答 解:∵$\frac{1}{2}$(x+2)-3>0,
解之得x>4,
而x>m,
并且不等式组解集为x>4,
∴m≤4.
故选A.
点评 本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解),

练习册系列答案
相关题目
12.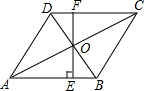 如图,在菱形ABCD中,对角线C,BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD点F,则AE的长( )
如图,在菱形ABCD中,对角线C,BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD点F,则AE的长( )
 如图,在菱形ABCD中,对角线C,BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD点F,则AE的长( )
如图,在菱形ABCD中,对角线C,BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD点F,则AE的长( )| A. | 4 | B. | 4.8 | C. | 2.4 | D. | 3.2 |
13.若A(-1,y1),B(-5,y2),C(0,y3)为二次函数y=x2+4x-5的图象上的三点,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y1<y3<y2 |
10.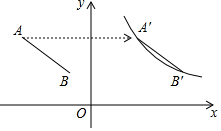 如图,已知A(-3,3),B(-1,1.5),将线段AB向右平移d个单位长度后,点A、B恰好同时落在反比例函数y=$\frac{6}{x}$(x>0)的图象上,则d等于( )
如图,已知A(-3,3),B(-1,1.5),将线段AB向右平移d个单位长度后,点A、B恰好同时落在反比例函数y=$\frac{6}{x}$(x>0)的图象上,则d等于( )
 如图,已知A(-3,3),B(-1,1.5),将线段AB向右平移d个单位长度后,点A、B恰好同时落在反比例函数y=$\frac{6}{x}$(x>0)的图象上,则d等于( )
如图,已知A(-3,3),B(-1,1.5),将线段AB向右平移d个单位长度后,点A、B恰好同时落在反比例函数y=$\frac{6}{x}$(x>0)的图象上,则d等于( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
17.下列命题中,真命题是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 一组对边相等,一组对角相等的四边形是平行四边形 | |
| D. | 一组对边平行,一组对角相等的四边形是平行四边形 |
7.下列各式$\frac{2}{x}$,$\frac{{x}^{2}}{{x}^{3}}$,$\frac{1}{2}$x2y,$\frac{{a}^{2}{b}^{2}}{4}$,$\frac{1}{a+5}$,$\frac{m+a}{π}$中,是分式的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.下列实数中,无理数是( )
| A. | 2 | B. | 3.333 | C. | -π | D. | $\sqrt{4}$ |
11.下列计算正确的是( )
| A. | (-2a2)3=8a6 | B. | (-$\frac{1}{2}$)-1=$\frac{1}{2}$ | C. | $\sqrt{9}$=±3 | D. | a10÷a5=a5 |
12.计算(-1+2)×(-$\frac{1}{2}$)2÷(-2)的结果是( )
| A. | 8 | B. | -8 | C. | $\frac{1}{8}$ | D. | $-\frac{1}{8}$ |