题目内容
17. 如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=2,AC=3,则tanB的值是$\frac{{3\sqrt{7}}}{7}$.
如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=2,AC=3,则tanB的值是$\frac{{3\sqrt{7}}}{7}$.
分析 根据直角三角形斜边上的中线等于斜边的一半求出AB的长度,再利用勾股定理求出BC的长度,然后根据锐角的正切等于对边比邻边解答.
解答 解:∵CD是斜边AB上的中线,CD=2,
∴AB=2CD=4,
根据勾股定理,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{7}$,
tanB=$\frac{AC}{BC}$=$\frac{3}{\sqrt{7}}$=$\frac{3\sqrt{7}}{7}$.
故答案为:$\frac{{3\sqrt{7}}}{7}$.
点评 本题考查了锐角三角函数的定义,直角三角形斜边上的中线等于斜边的一半的性质,勾股定理的应用,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边应熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.下列结论中正确的个数是( )
(1)(-$\sqrt{5}$+$\sqrt{3}$)0=1
(2)[(x2)3]2=x8
(3)(a+b)(b+a)=a2+2ab+b2
(4)(-2a)3÷a=-8a2.
(1)(-$\sqrt{5}$+$\sqrt{3}$)0=1
(2)[(x2)3]2=x8
(3)(a+b)(b+a)=a2+2ab+b2
(4)(-2a)3÷a=-8a2.
| A. | 1 | B. | 3 | C. | 2 | D. | 4 |
12.今年国庆长假期间,涪洋镇“家家福”超市某商品按标价打八折销售,小玲购了一件该商品,付款56元,则该项商品的标价为( )元.
| A. | 56 | B. | 68 | C. | 70 | D. | 72 |
7.下列说法正确的是( )
| A. | 8的立方根是2 | B. | -4的平方根是-2 | C. | 16的平方根是 4 | D. | 1的立方根是±1 |
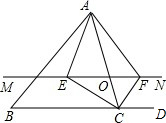 如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACD平分线于点F.
如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACD平分线于点F. 如图所示,在△ABC中,AC=9cm,DE垂直平分AB,如果△DBC的周长是16cm,那么BC的长度为7cm.
如图所示,在△ABC中,AC=9cm,DE垂直平分AB,如果△DBC的周长是16cm,那么BC的长度为7cm.