题目内容
14.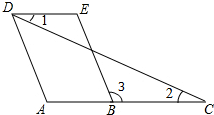 已知,如图,AD∥BE,∠1=∠2,求证:∠A=∠E.
已知,如图,AD∥BE,∠1=∠2,求证:∠A=∠E.证明:∵AD∥BE(已知),
∴∠A=∠3(两直线平行,同位角相等)
又∵∠1=∠2( 已知 ),
∴AC∥DE(内错角相等,两直线平行),
∴∠3=∠E(两直线平行,内错角相等),
∴∠A=∠E(等量代换).
分析 先根据平行线的性质由AD∥BE得∠A=∠EBC,再根据平行线的判定由∠1=∠2得DE∥AC,则∠E=∠EBC,所以∠A=∠E.
解答 证明:∵AD∥BE(已知),
∴∠A=∠_3__(两直线平行,同位角相等),
又∵∠1=∠2(已知)
∴AC∥DE(内错角相等,两直线平行),
∵∠3=∠E(两直线平行,内错角相等),
∴∠A=∠E(等量代换).
故答案为:3,两直线平行,同位角相等,DE,内错角相等,两直线平行,E,两直线平行,内错角相等.
点评 本题考查了平行线性质和判定,熟练掌握平行线的性质和判定定理是解题的关键.

练习册系列答案
相关题目
4.用科学记数法表示52000000正确的是( )
| A. | 52×107 | B. | 5.2×108 | C. | 5.2×107 | D. | 52×108 |
2.因春节放假,某工厂2月份产量比1月份下降了5%,3月份将恢复正常,预计3月份产量将比2月份增长15%.设2、3月份的平均增长率为x,则x满足的方程是( )
| A. | 15%-5%=x | B. | 15%-5%=2x | C. | (1-5%)(1+15%)=2(1+x) | D. | (1-5%)(1+15%)=(1+x)2 |
9.式子$\sqrt{{2}^{2}}$的值是( )
| A. | 4 | B. | 2 | C. | ±2 | D. | -2 |
19.已知$\frac{1}{x}$-$\frac{1}{y}$=3,则分式$\frac{2x+3xy-2y}{x-2xy-y}$的值为( )
| A. | $\frac{3}{5}$ | B. | -3 | C. | 9 | D. | -$\frac{9}{5}$ |
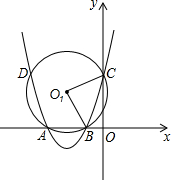 如图,抛物线y=ax2+bx+3过点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1经过A,B,C三点,与抛物线相交于另一点D.
如图,抛物线y=ax2+bx+3过点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1经过A,B,C三点,与抛物线相交于另一点D.