题目内容
8.将一块正方形和一块等腰直角三角形如图1摆放.(1)如果把图1中的△BCN绕点B逆时针旋转90°,得到图2,则∠GBM=45°;
(2)将△BEF绕点B旋转.
①当M,N分别在AD,CD上(不与A,D,C重合)时,线段AM,MN,NC之间有一个不变的相等关系式,请你写出这个关系式:MN=AM+CN;(不用证明)
②当点M在AD的延长线上,点N在DC的延长线时(如图3),①中的关系式是否仍然成立?若成立,写出你的结论,并说明理由;若不成立,写出你认为成立的结论,并说明理由.

分析 (1)由旋转的性质得∠GBA=∠CBN,于是得到∠ABM+∠GBA=45°,即可得到结论;
(2)①根据旋转的性质得到∠GAB=∠C=90°,AG=CN,BG=BN,∠ABG=∠CBN,得到D,A,G三点共线,根据全等三角形的性质得到GM=MN,于是得到结论;
②在AM上截取AG,使得AG=CN,连结BG;根据正方形的性质得到AB=BC,∠A=∠BCN=90°,根据全等三角形的性质得到BG=BN,∠ABG=∠NBC,根据全等三角形的性质即可得到结论.
解答 解:(1)在正方形ABCD和等腰直角△BEF中,
∵∠ABC=90°,
∴∠EBF=45°,
∴∠ABM+∠CBN=45°,
由旋转的性质得∠GBA=∠CBN,
∴∠ABM+∠GBA=45°,
即∠GBM=45°,
故答案为:45°;
(2)①AM+NC=MN;
理由:∵把图1中的△BCN绕点B逆时针旋转90°得到△ABG,
∴∠GAB=∠C=90°,AG=CN,BG=BN,∠ABG=∠CBN,
∴∠GAB+∠DAB=180°,
∴D,A,G三点共线,
∴∠ABM+∠GBA=45°,
∴∠GBM=∠MBN,
在△GBM与△NBM中,$\left\{\begin{array}{l}{BG=BC}\\{∠GBM=∠CBM}\\{BM=BM}\end{array}\right.$,
∴△GBM≌△NBM,
∴GM=MN,
∵GM=AG+AM=CN+AM,
∴MN=AM+CN;
故答案为:MN=AM+CN;
②上面的式子不成立,结论是:AM-NC=MN,
理由:在AM上截取AG,使得AG=CN,连结BG;
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠BCN=90°,
在△BAG与△BCN中,$\left\{\begin{array}{l}{AB=BC}\\{∠A=∠BCN=90°}\\{AG=CN}\end{array}\right.$,
∴△BAG≌△BCN,
∴BG=BN,∠ABG=∠NBC,
∴∠MBN=∠MBC+∠CBN=∠MBC+∠ABG=45°=∠GBM,
在△BGM与△BMN中,
$\left\{\begin{array}{l}{BG=BN}\\{∠GBM=∠NBM}\\{BM=BM}\end{array}\right.$,
∴△BGM≌△BNM,
∴GM=NM,
∴AM-CN=MN.
点评 本题考查了旋转的性质,全等三角形的判定和性质,正方形的性质,等腰直角三角形的性质,正确的作出辅助线是解题的关键.

 名校课堂系列答案
名校课堂系列答案




 如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=1,OC=$\frac{1}{2}$,在第二象限内,以原点O为位似中心将矩形AOCB放大为原来的$\frac{3}{2}$倍,得到矩形A1OC1B1,再以原点O为位似中心将矩形
如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=1,OC=$\frac{1}{2}$,在第二象限内,以原点O为位似中心将矩形AOCB放大为原来的$\frac{3}{2}$倍,得到矩形A1OC1B1,再以原点O为位似中心将矩形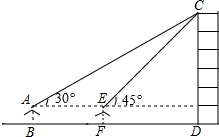 某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,测量一建筑物CD的高度,他们站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走20m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知观测员的眼睛与地面距离为1.5m(即AB=1.5m),求这栋建筑物CD的高度.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数)
某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,测量一建筑物CD的高度,他们站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走20m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知观测员的眼睛与地面距离为1.5m(即AB=1.5m),求这栋建筑物CD的高度.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数)