Question

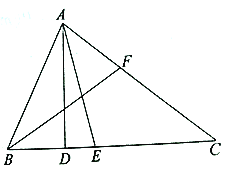
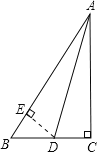
【题目】△ABC中，∠C＝90°，∠BAC的平分线交BC于D，且CD＝15，AC＝30，求AB的长．

Answer 1

【答案】50

【解析】

作DE⊥AB于点E，由得出，然后证得△ABC∽△DBE，则,设BD＝x，BE＝y，则，解得x＝2y﹣15，在Rt△DBE中，BD2＝DE2+BE2，即（2y﹣15）2＝y2+152，求得y的值，即可求得AB．

解：如图，作DE⊥AB于点E，则∠BED＝90°，

∵AD平分

在和中，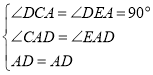

∴

∴∠BED＝∠C＝90°，

∵∠EBD＝∠ABC，

∴△ABC∽△DBE，

∴，

设BD＝x，BE＝y，

则，

∴x＝2y﹣15，

在Rt△DBE中，BD2＝DE2+BE2，

即（2y﹣15）2＝y2+152，

∴y＝20，

AB＝AE+BE＝30+20＝50．

故答案为：50．