Question

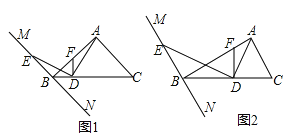
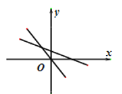
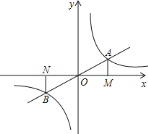
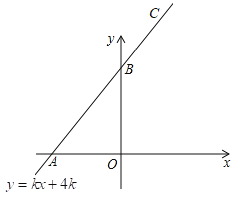
【题目】如图，一次函数的图像与轴交于点，与轴交于点，且经过点．

(1)当时；

①求一次函数的表达式；

②平分交轴于点，求点的坐标；

(2)若△为等腰三角形，求的值；

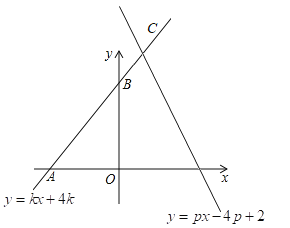
(3)若直线也经过点，且，求的取值范围．

Answer 1

【答案】(1)①；②（-，0）；(2) ；(3) .

【解析】

(1)①把x=2,y=代入中求出k值即可；

②作DE⊥AB于E，先求出点A、点B坐标，继而求出OA、OB、AB的长度,由角平分线的性质可得到OD=DE,于是BE=OB可求BE、AE的长,然后在中用勾股定理可列方程，解方程即可求得OD的长；

(2)求得点A坐标是（-4，0），点C坐标是（2，），由△为等腰三角形,可知OC=OA=4,故,解方程即可；

(3) 由直线经过点， 得=,由（2）知,故,用k表示p代入中得到关于k的不等式，解不等式即可.

解：(1)当时，点C坐标是，

①把x=2,y=代入中，

得，

解得，

所以一次函数的表达式是；

②如图，平分交轴于点，作DE⊥AB于E，

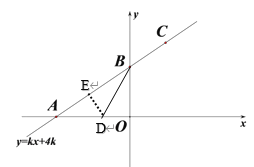
∵在中，当x=0时，y=3；当y=0时，x=-4，

∴点A坐标是（-4，0），点B坐标是（0，3），

∴OA=4,OB=3,

∴,

∵平分, DE⊥AB, DO⊥OB,

∴OD=DE,

∵BD=BD,

∴,

∴BE=OB=3,

∴AE=AB-BE=5-3=2,

∵在中，,

∴,

∴OD= ,

∴点D坐标是（-，0），

(2) ∵在中，当y=0时，x=-4；当x=2时，y=，

∴点A坐标是（-4，0），点C坐标是（2，），

∵△为等腰三角形,

∴OC=OA=4,

∴,

∴,（不合题意，舍去），

∴.

(3) ∵直线经过点，

∴=,

由（2）知,

∴,

∴,

∵,

∴,

∴.