题目内容
13.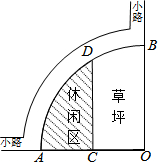 如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )| A. | $(6π-\frac{9}{2}\sqrt{3}){m^2}$ | B. | $(6π-9\sqrt{3}){m^2}$ | C. | $(π-\frac{9}{2}\sqrt{3}){m^2}$ | D. | $(10π-\frac{9}{2}\sqrt{3}){m^2}$ |
分析 先根据半径OA长是6米,C是OA的中点可知OC=$\frac{1}{2}$OA=3米,再在Rt△OCD中,利用勾股定理求出CD的长,根据锐角三角函数的定义求出∠DOC的度数,由S阴影=S扇形AOD-S△DOC即可得出结论.
解答 解:连接OD,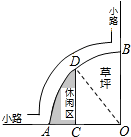
∵弧AB的半径OA长是6米,C是OA的中点,
∴OC=$\frac{1}{2}$OA=$\frac{1}{2}$×6=3米,
∵∠AOB=90°,CD∥OB,
∴CD⊥OA,
在Rt△OCD中,
∵OD=6,OC=3,
∴CD=$\sqrt{O{D}^{2}-O{C}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3 $\sqrt{3}$米,
∵sin∠DOC=$\frac{CD}{OD}$=$\frac{3\sqrt{3}}{6}$=$\frac{\sqrt{3}}{2}$,
∴∠DOC=60°,
∴S阴影=S扇形AOD-S△DOC=$\frac{60•π•{6}^{2}}{360}$-$\frac{1}{2}$×3×3 $\sqrt{3}$=(6π-$\frac{9\sqrt{3}}{2}$)平方米.
故选A.
点评 本题考查的是扇形的面积,根据题意求出∠DOC的度数,再由S阴影=S扇形AOD-S△DOC得出结论是解答此题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
16.某企业的年收入约为700000元,数据“700000”用科学记数法可表示为( )
| A. | 0.7×106 | B. | 7×105 | C. | 7×104 | D. | 70×104 |
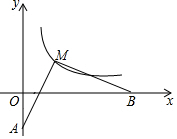 如图,点M为双曲线y=$\frac{k}{x}$(x>0)上一点,已知A(0,-1),B(5,0),若MA=MB,且MA⊥MB,求k的值.
如图,点M为双曲线y=$\frac{k}{x}$(x>0)上一点,已知A(0,-1),B(5,0),若MA=MB,且MA⊥MB,求k的值.
 如图,已知∠BAC及BA上一点P,求作直线MN,使MN经过点P,且MN∥AC.(要求:使用尺规正确作图,保留作图痕迹)
如图,已知∠BAC及BA上一点P,求作直线MN,使MN经过点P,且MN∥AC.(要求:使用尺规正确作图,保留作图痕迹)