题目内容
已知菱形ABCD,∠ABC=60°,O为AC边的中点,E为线段AC上一点(不与A、O、C点重合).
(1)如图1,当E点在线段AC上时,F点在边AD上,DF=CE,射线BE与CF交于M,连接AM,求证:MA平分∠EMF;
(2)当点E在线段AC上时,G点为E点关于O点的对称点,延长BE到P使EP=BE,点N为边AD上一点,并且满足AN=AC-EG,请你判断直线PN与直线AB的位置关系,并证明你的结论.
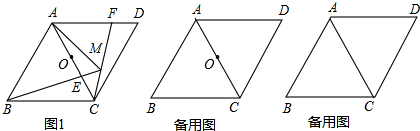
(1)如图1,当E点在线段AC上时,F点在边AD上,DF=CE,射线BE与CF交于M,连接AM,求证:MA平分∠EMF;
(2)当点E在线段AC上时,G点为E点关于O点的对称点,延长BE到P使EP=BE,点N为边AD上一点,并且满足AN=AC-EG,请你判断直线PN与直线AB的位置关系,并证明你的结论.

考点:菱形的性质
专题:
分析:(1)求出AF=AE,再利用“边角边”证明△ABE和△ACF全等,根据全等三角形对应角相等可得∠ABE=∠ACF,然后求出△ABE和△CME相似,根据相似三角形对应角相等可得∠CME=∠BAE=60°,相似三角形对应边成比例可得
=
,再求出△AEM和△BEC相似,根据相似三角形对应角相等可得∠AME=∠ACB=60°,再求出∠AMF=60°,然后根据角平分线的定义解答;
(2)连接NE并延长与AB相交于点F,根据对称性可得AE=CG,然后求出AN=2AE,再求出∠AEN=90°,根据菱形的对称性可得EN=EF,再利用“边角边”证明△BEF和△PEN全等,根据全等三角形对应角相等可得∠BFE=∠PNE,再根据内错角相等,两直线平行证明即可.
| AE |
| ME |
| BE |
| CE |
(2)连接NE并延长与AB相交于点F,根据对称性可得AE=CG,然后求出AN=2AE,再求出∠AEN=90°,根据菱形的对称性可得EN=EF,再利用“边角边”证明△BEF和△PEN全等,根据全等三角形对应角相等可得∠BFE=∠PNE,再根据内错角相等,两直线平行证明即可.
解答:(1)证明:∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,
又∵菱形的边AB=AD,DF=CE,
∴AD-AF=AC-CE,
即AF=AE,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴∠ABE=∠ACF,
∵∠AEB=∠CEM,
∴△ABE∽△CME,
∴∠CME=∠BAE=60°,
=
,
又∵∠AEM=∠BEC,
∴△AEM∽△BEC,
∴∠AME=∠ACB=60°,
∴∠AMF=180°-∠AME-∠CME=180°-60°-60°=60°,
∴∠AMF=∠AME,
∴MA平分∠EMF;
(2)解:PN∥AB.
理由如下:如图,连接NE并延长与AB相交于点F,
由菱形的对称性得,AE=CG,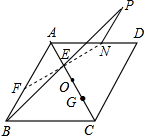
∵AN=AC-EG,
∴AN=2AE,
∵∠CAD=∠ACB=60°,
∴∠ANE=30°,∠AEN=90°,
由菱形的对称性得EN=EF,
在△BEF和△PEN中,
,
∴△BEF≌△PEN(SAS),
∴∠BFE=∠PNE,
∴PN∥AB.
∴△ABC是等边三角形,
∴AB=AC,
又∵菱形的边AB=AD,DF=CE,
∴AD-AF=AC-CE,
即AF=AE,
在△ABE和△ACF中,
|
∴△ABE≌△ACF(SAS),
∴∠ABE=∠ACF,
∵∠AEB=∠CEM,
∴△ABE∽△CME,
∴∠CME=∠BAE=60°,
| AE |
| ME |
| BE |
| CE |
又∵∠AEM=∠BEC,
∴△AEM∽△BEC,
∴∠AME=∠ACB=60°,
∴∠AMF=180°-∠AME-∠CME=180°-60°-60°=60°,
∴∠AMF=∠AME,
∴MA平分∠EMF;
(2)解:PN∥AB.
理由如下:如图,连接NE并延长与AB相交于点F,
由菱形的对称性得,AE=CG,

∵AN=AC-EG,
∴AN=2AE,
∵∠CAD=∠ACB=60°,
∴∠ANE=30°,∠AEN=90°,
由菱形的对称性得EN=EF,
在△BEF和△PEN中,
|
∴△BEF≌△PEN(SAS),
∴∠BFE=∠PNE,
∴PN∥AB.
点评:本题考查了菱形的性质,全等三角形的判定与性质,相似三角形的判定与性质,等边三角形的判定与性质,(1)求出相似三角形然后根据角的度数相等求解是解题的关键,(2)作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
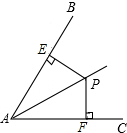 如图,点P是∠BAC内一点,且P到AB、AC的距离PE=PF,则下列哪一个能作为△PEA≌△PFA的理由( )
如图,点P是∠BAC内一点,且P到AB、AC的距离PE=PF,则下列哪一个能作为△PEA≌△PFA的理由( )| A、HL | B、AAS |
| C、SSS | D、ASA |
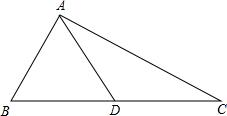 阅读理解题:
阅读理解题: 如图,在△ABC中,AB=AC,D是BC的中点,E是BA延长线上一点,F是AC上一点,且AE=AF,连接EF并延长交BC于点G,证明:AD∥EG.
如图,在△ABC中,AB=AC,D是BC的中点,E是BA延长线上一点,F是AC上一点,且AE=AF,连接EF并延长交BC于点G,证明:AD∥EG.