题目内容
18.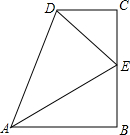 如图所示,AB∥CD,∠B=90°,E是BC的中点,DE平分∠ADC,求证:AE平分∠DAB.
如图所示,AB∥CD,∠B=90°,E是BC的中点,DE平分∠ADC,求证:AE平分∠DAB.
分析 过点E作EF⊥AD于F,根据角平分线上的点到角的两边距离相等可得CE=EF,根据线段中点的定义可得BE=CE,然后求出BE=EF,再根据到角的两边距离相等的点在角的平分线上证明即可.
解答  证明:如图,过点E作EF⊥AD于F,
证明:如图,过点E作EF⊥AD于F,
∵AB∥CD,∠B=90°,
∴∠C=180°-90°=90°,
∵DE平分∠ADC,
∴CE=EF,
∵E是BC的中点,
∴BE=CE,
∴BE=EF,
又∵∠B=90°,
∴点E在∠BAD的平分线上,
∴AE平分∠DAB.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,到角的两边距离相等的点在角的平分线上的性质,熟记各性质并作出辅助线是解题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
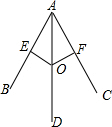 如图是雨伞开闭过程中某时刻的截面图,伞骨AB=AC,支撑杆OE=OF,AE=$\frac{1}{3}$AB,AF=$\frac{1}{3}$AC.当O沿AD滑动时,雨伞开闭.雨伞开闭过程中,∠BAD与∠CAD有何关系?请说明理由.
如图是雨伞开闭过程中某时刻的截面图,伞骨AB=AC,支撑杆OE=OF,AE=$\frac{1}{3}$AB,AF=$\frac{1}{3}$AC.当O沿AD滑动时,雨伞开闭.雨伞开闭过程中,∠BAD与∠CAD有何关系?请说明理由.