��Ŀ����
13����1����ͼ1����֪��ABC�������������ֱ�ΪA��1��4����B��4��1����C��4��4������˫����y=$\frac{k}{x}$��x��0�����ABC�й����㣬��k��ȡֵ��Χ��4��k��16����2����ͼ1�еġ�ABC��ֱ��AB���ۺ�õ���ABC1����˫����y=$\frac{m}{x}$��x��0�����ABC1�й����㣬��m��ȡֵ��Χ��
С������һԪ���η��̸����ж�ʽԲ���ؽ����������⣬С���������κ���ģ��ҲԲ���ؽ����������⣮��������ͼ2�л�����ABC1����д���Լ��Ľ����̣�
��3����ͼ3����֪��AΪ��1��2������BΪ��4��1������˫����y=$\frac{n}{x}$��x��0�����߶�AB�й����㣬��n��ȡֵ��Χ��2��n��$\frac{49}{12}$��
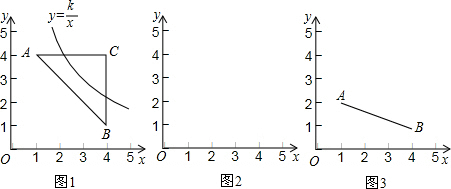
���� ��1���ֱ����˫����y=$\frac{k}{x}$��x��0�����AC����BC�й������k��ȡֵ��Χ��Ȼ�����ֱ��AB�Ľ���ʽ������һԪ���η��̸����б�ʽ������AB�й������k��ȡֵ��Χ�������ô𰸣�
��2��������õ�C�����꣬���ɵ�˫����y=$\frac{m}{x}$��x��0�����AC����BC�й������k��ȡֵ��Χ���ɣ�1����������AB��ȡֵ��Χ���̶���ô𰸣�
��3����������߶�AB�Ľ���ʽ�Լ��Ա�����ȡֵ��Χ��������һԪ���η��̸����б�ʽ��ô𰸣�
��� �⣺��1����ֱ��AB�Ľ���ʽΪ��y=kx+b��
��A��1��4����B��4��1����
��$\left\{\begin{array}{l}{k+b=4}\\{4k+b=1}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪ��y=-x+5��
�ߡ�ABC�������������ֱ�ΪA��1��4����B��4��1����C��4��4����
����˫����y=$\frac{k}{x}$��x��0�����AC�й����㣬��4��k��16��
��˫����y=$\frac{k}{x}$��x��0�����BC�й����㣬��4��k��16��
��˫����y=$\frac{k}{x}$��x��0�����AB�й����㣬��$\frac{k}{x}$=-x+5��1��x��4����
��x2-5x+k=0��
���=25-4k��0��
��ã�k��$\frac{25}{4}$��
����˫����y=$\frac{k}{x}$��x��0�����AB�й����㣬��4��k��$\frac{25}{4}$��
���Ͽɵã���˫����y=$\frac{k}{x}$��x��0�����ABC�й����㣬��k��ȡֵ��Χ�ǣ�4��k��16��
�ʴ�Ϊ��4��k��16��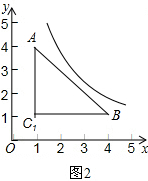 ��2����ͼ�����C1��1��1����
��2����ͼ�����C1��1��1����
�ɣ�1���ã���˫����y=$\frac{m}{x}$��x��0�����AB�й����㣬��4��m��$\frac{25}{4}$��
����˫����y=$\frac{m}{x}$��x��0�����AC�й����㣬��1��k��4��
��˫����y=$\frac{m}{x}$��x��0�����BC�й����㣬��1��k��4��
���Ͽɵã���˫����y=$\frac{m}{x}$��x��0�����ABC�й����㣬��k��ȡֵ��Χ�ǣ�1��k��$\frac{25}{4}$��
��3����ͼ3����ֱ��AB�Ľ���ʽΪ��y=mx+n��
�ߵ�AΪ��1��2������BΪ��4��1����
��$\left\{\begin{array}{l}{m+n=2}\\{4m+n=1}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{m=-\frac{1}{3}}\\{n=\frac{7}{3}}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪ��y=-$\frac{1}{3}$x+$\frac{7}{3}$��1��x��4����
��˫����y=$\frac{n}{x}$��x��0�����߶�AB�й����㣬
��$\frac{n}{x}$=-$\frac{1}{3}$x+$\frac{7}{3}$��
�����ã�x2-7x+3n=0��
���=49-12n��0��
��n��$\frac{49}{12}$��
��1��x��4��
��n��2��
����˫����y=$\frac{n}{x}$��x��0�����߶�AB�й����㣬��n��ȡֵ��Χ�ǣ�2��n��$\frac{49}{12}$��
�ʴ�Ϊ��2��n��$\frac{49}{12}$��
���� �������ڷ����������ۺ��⣬������ֱ���뷴���������Ľ��������Լ�һԪ���η��̵ĸ����б�ʽ��ע���ܽ���һԪ���η��̸����ж�ʽ����ǹؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | -3 | B�� | 3 | C�� | -$\frac{1}{3}$ | D�� | $\frac{1}{3}$ |
| A�� | $\sqrt{4}$=��2 | B�� | 3-1=-$\frac{1}{3}$ | C�� | ��-1��2015=-1 | D�� | |-2|=-2 |
| A�� | 30 | B�� | 26 | C�� | 10 | D�� | 6 |
| A�� | 2��2 | B�� | 2��3 | C�� | 3��4 | D�� | 4��4 |
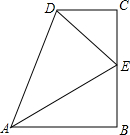 ��ͼ��ʾ��AB��CD����B=90�㣬E��BC���е㣬DEƽ�֡�ADC����֤��AEƽ�֡�DAB��
��ͼ��ʾ��AB��CD����B=90�㣬E��BC���е㣬DEƽ�֡�ADC����֤��AEƽ�֡�DAB��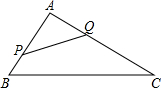 ��ͼ����������ABC�У�AB=8��AC=16����P�ӵ�B��ʼ�ر�BA���A��2����ÿ����ٶ��ƶ�����Q�ӵ�A���C��4����ÿ����ٶ��ƶ��������P��Q�ֱ�ӵ�B��Aͬʱ����������������ʱ����A��P��QΪ�������������������ABC���ƣ�
��ͼ����������ABC�У�AB=8��AC=16����P�ӵ�B��ʼ�ر�BA���A��2����ÿ����ٶ��ƶ�����Q�ӵ�A���C��4����ÿ����ٶ��ƶ��������P��Q�ֱ�ӵ�B��Aͬʱ����������������ʱ����A��P��QΪ�������������������ABC���ƣ�