题目内容
7.玩具加工厂预计生产甲、乙两种玩具产品共50件,已知生产一件甲种玩具需要A种原料3个,B种原料6个,可获利80元;生产一件乙种玩具需要A种原料5个,B种原料5个,可获利100元,已知玩具加工厂现有A种原料220个,B种原料267个,假设生产甲种玩具x个,共获利y元.(1)请问有几种方案符合生产玩具的要求;
(2)请你写出y与x之间的函数关系,并用函数的知识来设计一个方案使得获利最大,最大利润是多少元?
分析 (1)根据“生产甲玩具时A原料总数量+生产乙玩具时A原料总数量≤220、生产甲玩具时B原料总数量+生产甲玩具时B原料总数量≤267”列出不等式组,解不等式组可得方案;
(2)根据“总利润=生产甲玩具的总利润+生产乙玩具的总利润”,列出函数关系式,结合(1)中x的范围和函数性质可知获利最大的方案.
解答 解:(1)根据题意知,生产甲种玩具x个,则乙玩具有(50-x)个,
得:$\left\{\begin{array}{l}{3x+5(50-x)≤220}\\{6x+5(50-x)≤267}\end{array}\right.$,
解得:15≤x≤17,
∵x为整数,
∴x可取15,16,17,
则有如下3中方案符合要求:
①甲玩具15件,乙玩具35件;
②甲玩具16件,乙玩具34件;
③甲玩具17件,乙玩具33件.
(2)根据题意,y=80x+100(50-x)=-20x+5000,
∵-20<0,
∴y随x的增大而减小,
又∵15≤x≤17,
∴当x=15时,获利最大,最大利润y=-20×15+5000=4700元,
即生产甲玩具15件,乙玩具35件时获利最大,最大利润为4700元.
点评 本题主要考查不等式组的应用和一次函数的应用能力,根据题意找到不等关系和相等关系是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

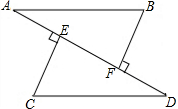 如图,已知AE=DF,AB∥CD,CE⊥AD,BF⊥AD.求证:
如图,已知AE=DF,AB∥CD,CE⊥AD,BF⊥AD.求证: 如图,在△ABC中,AD是BC边上的高,∠ABC=2∠C,E是AC的中点,ED的延长线交AB的延长线于点F.
如图,在△ABC中,AD是BC边上的高,∠ABC=2∠C,E是AC的中点,ED的延长线交AB的延长线于点F. 如图,△ABC,△DCE都为等腰直角三角形,B、C、E三点在同一直线上,BF∥DE,DF交BE于G,且G为BE的中点:
如图,△ABC,△DCE都为等腰直角三角形,B、C、E三点在同一直线上,BF∥DE,DF交BE于G,且G为BE的中点: