题目内容
7.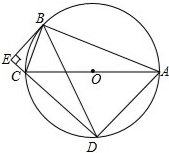 如图,⊙O是△ABC的外接圆,∠ABC=90°,BE⊥CE,BE是⊙O的切线交DC的延长线于点E.
如图,⊙O是△ABC的外接圆,∠ABC=90°,BE⊥CE,BE是⊙O的切线交DC的延长线于点E.(1)求证:BD=BA;
(2)若BC=3,⊙O的半径为$\frac{9}{2}$,求线段CD的长度.
分析 (1)连接OB,由切线得垂直,则OB∥DE,得内错角相等,利用圆内接四边形的一个外角等于内对角得出∠BCE=∠DAB;再利用同圆半径相等和等边对等角及同弧所对的圆周角相等得出∠ADB=∠DAB,利用等角对等边得出结论;
(2)利用两角对应相等证△BCE∽△ACB得出CE的长,由勾股定理分别在三个直角三角形求出AB、BE、DE,则CD=ED-CE.
解答 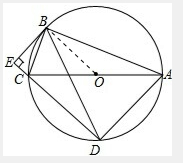 证明:(1)连接OB,
证明:(1)连接OB,
∵BE是⊙O的切线,
∴OB⊥BE,
∵BE⊥CE,
∴OB∥ED,
∴∠BCE=∠OBC,
∵OB=OC,
∴∠OCB=∠OBC,
∴∠BCE=∠OCB,
∵圆内接四边形ABCD,
∴∠BCE=∠DAB,
∵∠BCO=∠ADB,
∴∠ADB=∠DAB,
∴BD=BA;
(2)∵∠ABC=90°,
∴AC是⊙O的直径,AC=2A0=9,
在Rt△ABC中,∵BC=3,
∴AB=$\sqrt{{9}^{2}-{3}^{2}}$=6$\sqrt{2}$,
∴BD=AB=6$\sqrt{2}$,
∵∠E=∠ABC=90°,∠BCE=∠ACB,
∴△BCE∽△ACB,
∴$\frac{3}{9}$=$\frac{CE}{3}$,
∴CE=1,
在Rt△BCE中,AE=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$,
在Rt△BDE中,ED=$\sqrt{(6\sqrt{2})^{2}-(2\sqrt{2})^{2}}$=$\sqrt{64}$=8,
∴CD=ED-EC=8-1=7.
点评 本题考查了切线的性质和三角形的外接圆,在圆中证明两条弦相等,通常都证这两条弦所对的圆周角相等;本题已知切线这一条件,因此都要连接切点和圆心,利用切线的性质得垂直关系,另外在圆中求边长的方法:①利用勾股定理;②相似三角形.

练习册系列答案
相关题目
15.如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图(当AQI不大于100时称空气质量为“优良”),由图可得下列说法:①18日的PM2.5浓度最低;②这六天中PM2.5浓度的中位数是112?g/cm2;③这六天中有4天空气质量为“优良”;④空气质量指数AQI与PM2.5浓度有关,其中正确的说法是( )

| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
2.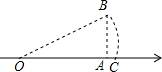 如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以原点O为圆心,OB为半径画弧,交数轴于点C,则OC的长为( )
如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以原点O为圆心,OB为半径画弧,交数轴于点C,则OC的长为( )
 如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以原点O为圆心,OB为半径画弧,交数轴于点C,则OC的长为( )
如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以原点O为圆心,OB为半径画弧,交数轴于点C,则OC的长为( )| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
17.等腰三角形有一个角是90°,则另两个角分别是( )
| A. | 30°,60° | B. | 45°,45° | C. | 45°,90° | D. | 20°,70° |
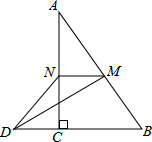 如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD,连接DM、DN、MN.若AB=6,则DN=3.
如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD,连接DM、DN、MN.若AB=6,则DN=3.