题目内容
11．先化简，再求值：（a-b）2+（a+3b）（a-3b）-a（a-2b），其中a=-1，b=2．分析 根据完全平方公式、平方差公式和单项式乘以多项式可以对原式化简，然后将a=-1，b=2代入即可解答本题．
解答 解：（a-b）2+（a+3b）（a-3b）-a（a-2b）
=a2-2ab+b2+a2-9b2-a2+2ab
=a2-8b2，
当a=-1，b=2时，原式=（-1）2-8×22=1-32=-31．
点评 本题考查整式的混合运算-化简求值，解题的关键是明确整式的混合运算的计算方法．
练习册系列答案
相关题目
1．若x的算术平方根为8，则它的立方根是（ ）
| A． | 2 | B． | -2 | C． | 4 | D． | ±4 |
2．
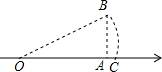如图，数轴上点A对应的数为2，AB⊥OA于A，且AB=1，以原点O为圆心，OB为半径画弧，交数轴于点C，则OC的长为（ ）
如图，数轴上点A对应的数为2，AB⊥OA于A，且AB=1，以原点O为圆心，OB为半径画弧，交数轴于点C，则OC的长为（ ）| A． | 2 | B． | 3 | C． | $\sqrt{3}$ | D． | $\sqrt{5}$ |
6．下面计算正确的是（ ）
| A． | 6a-5a=1 | B． | a2+a2=2a4 | C． | -（a-b）=-a+b | D． | 2（a+b）=2a+b |
3．
某公司招聘人才，对应聘者分别进行阅读能力、思维能力和表达能力三项测试，其中甲、乙两人的成绩如表（单位：分）：
（1）若根据三项测试的平均成绩在甲、乙两人中录用一人，那么谁将能被录用？
（2）根据实际需要，公司将阅读、思维和表达能力三项测试得分按3：5：2的比确定每人的最后成绩，若按此成绩在甲、乙两人中录用一人，谁将被录用？
（3）公司按照（2）中的成绩计算方法，将每位应聘者的最后成绩绘制成如图所示的频数分布直方图（每组分数段均包含左端数值，不包含右端数值，如最右边一组分数x为：85≤x＜90），并决定由高分到低分录用8名员工，甲、乙两人能否被录用？请说明理由，并求出本次招聘人才的录用率．
某公司招聘人才，对应聘者分别进行阅读能力、思维能力和表达能力三项测试，其中甲、乙两人的成绩如表（单位：分）：| 项目人员 | 阅读能力 | 思维能力 | 表达能力 |
| 甲 | 93 | 86 | 73 |
| 乙 | 95 | 81 | 79 |
（2）根据实际需要，公司将阅读、思维和表达能力三项测试得分按3：5：2的比确定每人的最后成绩，若按此成绩在甲、乙两人中录用一人，谁将被录用？
（3）公司按照（2）中的成绩计算方法，将每位应聘者的最后成绩绘制成如图所示的频数分布直方图（每组分数段均包含左端数值，不包含右端数值，如最右边一组分数x为：85≤x＜90），并决定由高分到低分录用8名员工，甲、乙两人能否被录用？请说明理由，并求出本次招聘人才的录用率．