题目内容
19.已知a=$\frac{\root{4}{64-{b}^{3}}+\root{4}{{b}^{3}-64}}{3}$-2,求a2+b2的平方根.分析 根据被开方数互为相反数,可得被开方数为零,可得a、b的值,根据有理数的运算,可得答案.
解答 解:由a=$\frac{\root{4}{64-{b}^{3}}+\root{4}{{b}^{3}-64}}{3}$-2,得
b3-64=64-b3=0,
解得b=4,a=-2.
a2+b2=16+4=20,
a2+b2的平方根=$±\sqrt{20}$=$±2\sqrt{5}$.
点评 本题考查了实数,利用被开方数互为相反数得出被开方数为零是解题关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
11.如果$\sqrt{24}$•$\sqrt{x}$是一个整数,那么x可取的最小正整数的值为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 12 |
8.若直线y=kx-b(b>0)与x轴交于点(-4,0),则当y>0时,x的取值范围( )
| A. | x>-4 | B. | x>0 | C. | x<-4 | D. | x<0 |
 直线y=kx-4与x轴、y轴分别交于B、C两点,且$\frac{OC}{OB}$=$\frac{4}{3}$.
直线y=kx-4与x轴、y轴分别交于B、C两点,且$\frac{OC}{OB}$=$\frac{4}{3}$.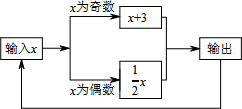 有一数值转换机,原理如图所示,若输入的x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2016次输出的结果是2.
有一数值转换机,原理如图所示,若输入的x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2016次输出的结果是2. 如图,矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(4,0),点B(0,3),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,连接OQ,设BP=t.
如图,矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(4,0),点B(0,3),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,连接OQ,设BP=t.