题目内容
7.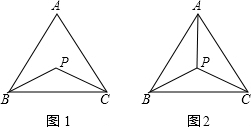 已知P是△ABC内任意一点.
已知P是△ABC内任意一点.(1)如图1,求证:AB+AC>PB+PC;
(2)如图2,连接PA,比较AB+AC+BC与PA+PB+PC的大小关系.
分析 (1)延长BP,交AC于D.在△ABD中,根据三角形两边之和大于第三边可得AB+AD>BP+PD,同理在△PCD中,可得PD+DC>PC,再根据不等式的性质得到AB+AD+PD+PC>BP+PD+PC,进而即可证明AB+AC>PB+PC;
(2)在三个三角形中分别利用三边关系列出三个不等式,相加后即可得到正确的结论;
解答 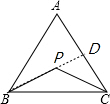 解:(1)证明:如图,延长BP,交AC于D.
解:(1)证明:如图,延长BP,交AC于D.
在△ABD中,AB+AD>BP+PD,
在△PCD中,PD+DC>PC,
所以AB+AD+PD+DC>BP+PD+PC,
即AB+AC>PB+PC;
(2)PA+PB+PC>$\frac{1}{2}$(AB+BC+AC).
理由:如图所示,在△ABP中,AP+BP>AB.
同理:BP+PC>BC,AP+PC>AC.
以上三式分别相加得到:
2(PA+PB+PC)>AB+BC+AC,
即PA+PB+PC>$\frac{1}{2}$(AB+BC+AC).
点评 本题考查的是三角形的三边关系,熟知三角形任意两边之和大于第三边是解答此题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
17.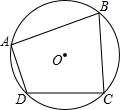 如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D-∠A的度数差为( )
如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D-∠A的度数差为( )
 如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D-∠A的度数差为( )
如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D-∠A的度数差为( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
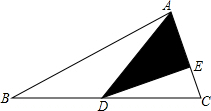 如图,△ABC中,D是BC的中点,AE=2CE,△ADE的面积比△CDE多1cm2,求△ABC的面积.
如图,△ABC中,D是BC的中点,AE=2CE,△ADE的面积比△CDE多1cm2,求△ABC的面积. 如图所示,长方形内有两个相邻的正方形,面积分别为3和5,那么阴影部分的面积为$\sqrt{15}$-3.
如图所示,长方形内有两个相邻的正方形,面积分别为3和5,那么阴影部分的面积为$\sqrt{15}$-3.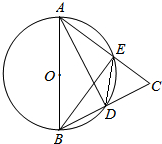 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D.求证:
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D.求证: