题目内容
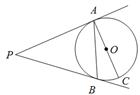
如图,在⊙O中,直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点D。求BC和AD的长。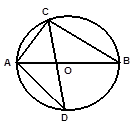
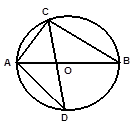
BC=8,AD=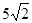
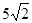
试题分析:在⊙O中,直径AB=10,那么
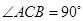 ,在直角三角形ABC中,由勾股定理得
,在直角三角形ABC中,由勾股定理得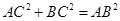 ,因为弦AC=6,所以
,因为弦AC=6,所以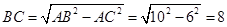
∠ACB的平分线交⊙O于点D,
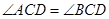 ,因为在⊙O中,直径AB=10,那么
,因为在⊙O中,直径AB=10,那么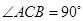 ,所以
,所以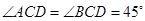 ,弧AD所对的圆周角是
,弧AD所对的圆周角是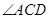 ,弧BD所对的圆周角是
,弧BD所对的圆周角是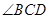 ,因为AB是⊙O的直径,所以可得出D是弧AB的中点,AD=BD;又因为AB是⊙O的直径,所以
,因为AB是⊙O的直径,所以可得出D是弧AB的中点,AD=BD;又因为AB是⊙O的直径,所以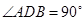 ,在直角三角形ABD中,由勾股定理可得
,在直角三角形ABD中,由勾股定理可得 ,解得
,解得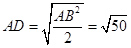 =
=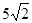
点评:本题考查平分线,圆,勾股定理,本题考查平分线的性质,圆的直径所对的圆周角为直角,勾股定理的内容

练习册系列答案
相关题目
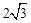 .则S阴影=
.则S阴影= 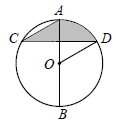
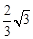
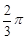



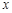 °,∠ECD=
°,∠ECD=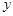 °,⊙B的半径为R,则
°,⊙B的半径为R,则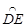 的长度是( )
的长度是( )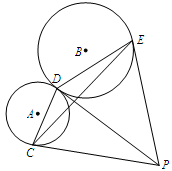




 是Rt
是Rt ABC的外接圆,
ABC的外接圆, ABC=90
ABC=90 ,点P是
,点P是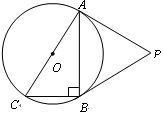
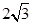 ,BC=2,求
,BC=2,求 中,半径长
中,半径长 ,
, ;以
;以 为直径作半圆
为直径作半圆 ,点
,点 是弧
是弧 上的一个动点,
上的一个动点, 与半圆
与半圆 ,
, ⊥
⊥ ,
, 交于点
交于点 ,连结
,连结 .
.
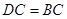 ;
; ,
,  ,试求
,试求 关于
关于 的函数关系式,并写出
的函数关系式,并写出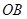 上,当
上,当 ∽
∽ 的长度.
的长度.