题目内容
1．
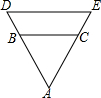如图，若BC∥DE，$\frac{AB}{AD}$=$\frac{3}{4}$，S△ABC=4，则四边形BCED的面积S四边形DBCE=$\frac{28}{9}$．
分析 因为DE∥BC，所以可得△ADE∽△ABC，根据相似三角形的面积比等于相似比的平方解答即可．
解答 解：∵D、E分别是△ABC的AB、AC边上的点，DE∥BC，
∴△ADE∽△ABC，
∵AB：AD=3：4，
∴S△ABC：S△ADE=9：16，
∴S四边形DBCE：S△ABC=7：9，
∵△ABC的面积为4，
∴四边形DBCE的面积为$\frac{28}{9}$．
故答案为：$\frac{28}{9}$．
点评 本题考查的是相似三角形的判定和性质，掌握相似三角形的面积的比等于相似比的平方是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．下列等式变形正确的是（ ）
| A． | 如果s=vt，那么v=$\frac{t}{s}$ | B． | 如果$\frac{1}{2}$x=6，那么x=3 | ||
| C． | 如果x-3=y-3，那么x=y | D． | 如果a=b，那么$\frac{1}{2}$a=2b |
如图，已知∠DAB=∠DCB，AF平分∠DAB，CE平分∠DCB，若AB∥CD，试判断
6．下列多项式能用平方差公式因式分解的是（ ）
| A． | 2x2-y2 | B． | x2-x-2 | C． | a2-4a+4 | D． | -1+a2 |
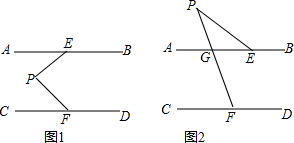
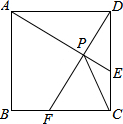如图，在正方形ABCD中，动点E，F分别从D，C两点同时出发，以相同的速度在边DC，CB上移动，连接AE和DF交于点P，由于点E，F的移动，使得点P也随之运动．若AD=2，线段CP的最小值是$\sqrt{5}$-1．
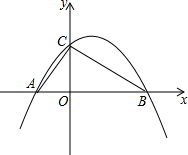如图，已知抛物线y=ax2+bx+c经过A（-2，0），B（4，0），C（0，3）三点．