题目内容
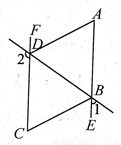
4. 如图:AC是⊙O的弦,AB是⊙O的切线,C,P在圆上.求证:∠BAC=∠P.
如图:AC是⊙O的弦,AB是⊙O的切线,C,P在圆上.求证:∠BAC=∠P.
分析 过点A作直径AD,连结CD,如图,由圆周角定理得到∠ACD=90°,则∠D+∠1=90°,再根据切线的性质得∠BAD=90°,即∠1+∠BAC=90°,所以∠BAC=∠D,接着根据圆周角定理有∠D=∠P,于是得到∠BAC=∠P.
解答 证明:过点A作直径AD,连结CD,如图,
∵AD为直径,
∴∠ACD=90°,
∴∠D+∠1=90°,
∵AB是⊙O的切线,
∴AD⊥AB,
∴∠BAD=90°,即∠1+∠BAC=90°,
∴∠BAC=∠D,
∵∠D=∠P,
∴∠BAC=∠P.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了圆周角定理.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
14.下列每组中的两个代数式,属于同类项的是( )
| A. | $\frac{1}{2}$x2y与$\frac{2}{3}$xy2 | B. | $\frac{1}{2}$m3n与-8nm3 | C. | 3abc与3ab | D. | 0.5a2b与0.5a2c |
 如图,在四边形ABCD中,AD=BC,∠ADC=∠BCD,求证:∠DAB=∠CBA.
如图,在四边形ABCD中,AD=BC,∠ADC=∠BCD,求证:∠DAB=∠CBA. 如图,已知线段AB,按下列要求作图:分别以点A,B为圆心,以任意长为半径(大于AB的一半)作弧,两弧相交于点C,D.
如图,已知线段AB,按下列要求作图:分别以点A,B为圆心,以任意长为半径(大于AB的一半)作弧,两弧相交于点C,D.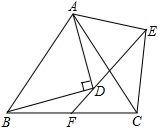 △ABC与△ADE都是以点A为顶点的等腰三角形,且∠BAC=∠DAE,BD⊥AD,ED的延长线交BC于点F,
△ABC与△ADE都是以点A为顶点的等腰三角形,且∠BAC=∠DAE,BD⊥AD,ED的延长线交BC于点F,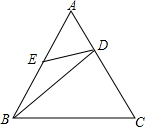 如图,在等边角形ABC中,点D,E分别在AC,AB边上,且$\frac{AD}{AC}$=$\frac{1}{3}$,AE=BE,接DE,BD.求证:∠AED=∠CBD.
如图,在等边角形ABC中,点D,E分别在AC,AB边上,且$\frac{AD}{AC}$=$\frac{1}{3}$,AE=BE,接DE,BD.求证:∠AED=∠CBD. 如图,已知直线MN与MN异侧两点A、B,在MN上求作一点P,使PA-PB最大.
如图,已知直线MN与MN异侧两点A、B,在MN上求作一点P,使PA-PB最大.