题目内容
20.已知函数y=x2+kx-3(k>0)图象的顶点坐标为C,并与x轴相交于A、B,且AB=4.(1)求实数k的值;
(2)若P是上述抛物线上的一个动点(除点C外),求使S△ABP=S△ABC成立的点P的坐标.
分析 (1)设抛物线与x轴的交点坐标是(x1,0)和(x2,0).则x1+x2=-k,x1•x2=-3.根据AB=4,即可列方程求得k的值;
(2)首先求得C的坐标,根据S△ABP=S△ABC,则P的纵坐标的绝对值与C的纵坐标的绝对值相等,据此即可求得P的坐标.
解答 解:(1)设抛物线与x轴的交点坐标是(x1,0)和(x2,0).
则x1+x2=-k,x1•x2=-3.
∵AB=|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{{k}^{2}+12}$=4,
∴k2+12=16,
∴k=2或-2.(舍去).
则k=2;
(2)y=x2+2x-3=(x+1)2-4,则抛物线顶点C的坐标是(-1,-4).
当y=4时,x2+2x-3=4,解得:x1=-1+2$\sqrt{2}$或x2=-1-2$\sqrt{2}$.
则P的坐标是(-1+2$\sqrt{2}$,4)或(-1-2$\sqrt{2}$,4).
点评 本题考查了二次函数以及一元二次方程根与系数的关系,正确求得k的值是关键.

练习册系列答案
相关题目
10.从2名男生和3名女生中随机抽取1名2015年苏州世乒赛志愿者,恰好抽到女生的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
11.方程$\frac{1}{x-1}-\frac{1}{x+1}=1$的解是( )
| A. | 1 | B. | -1 | C. | ±3 | D. | ±√3 |
5.下列一元二次方程中无实数解的是( )
| A. | x2+2x+1=0 | B. | x2=2x-1 | C. | x2+1=0 | D. | x2-4x-5=0 |

 如图,a、b为数轴上不同两点.则:
如图,a、b为数轴上不同两点.则: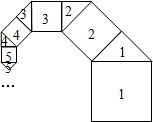 如图所示,第1个正方形的边是第1个等腰直角三角形的斜边,第1个等腰直角三角形的直角边是第2个正方形的边,第2个正方形的边是第2个等腰三角形的斜边…依此不断连接下去,设第1个正方形的边长为2,求:
如图所示,第1个正方形的边是第1个等腰直角三角形的斜边,第1个等腰直角三角形的直角边是第2个正方形的边,第2个正方形的边是第2个等腰三角形的斜边…依此不断连接下去,设第1个正方形的边长为2,求: