Question

10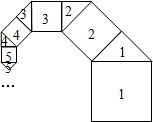．如图所示，第1个正方形的边是第1个等腰直角三角形的斜边，第1个等腰直角三角形的直角边是第2个正方形的边，第2个正方形的边是第2个等腰三角形的斜边…依此不断连接下去，设第1个正方形的边长为2，求：
（1）第2个正方形的边长a₂，面积S₂；
（2）第3个及第4个正方形的面积S₃，S₄；
（3）通过观察研究，写出第2003个正方形的面积S₂₀₀₃．

Answer 1

分析 设第1个正方形的边长a₁=2，然后根据等腰直角三角形的直角边等于斜边的$\frac{\sqrt{2}}{2}$倍依次求出第2、3、4个正方形的边长，然后根据变化规律写出第2003个正方形的边长，面积即可．

解答 解：第1个正方形的边长a₁=2，
（1）根据题意得，第2个正方形的边长为a₂=$\frac{\sqrt{2}}{2}$a₁=$\sqrt{2}$，面积S₂=（$\sqrt{2}$）²=2；
（2）第3个正方形的边长为a₃=$\frac{\sqrt{2}}{2}$a₂=$\frac{\sqrt{2}}{2}$（$\frac{\sqrt{2}}{2}$a₁）=（$\frac{\sqrt{2}}{2}$）²a₁=1，面积S₃=1；
第4个正方形的边长为a₄=$\frac{\sqrt{2}}{2}$a₃=$\frac{\sqrt{2}}{2}$（$\frac{\sqrt{2}}{2}$）²a₁=（$\frac{\sqrt{2}}{2}$）³a₁，=$\frac{\sqrt{2}}{2}$，面积S₄=$\frac{1}{2}$
…，
（3）第2003个正方形的边长a₂₀₀₃=（$\frac{\sqrt{2}}{2}$）²⁰⁰²a₁，
∵a₁=2，
∴a₂₀₀₃=2（$\frac{\sqrt{2}}{2}$）²⁰⁰²．面积S₂₀₀₃=4（$\frac{\sqrt{2}}{2}$）⁴⁰⁰⁴=$\frac{1}{{2}^{2000}}$

点评 本题考查了正方形的性质，等腰直角三角形的直角边与斜边的关系，根据变化规律求出指数与正方形的序数的关系是解题的关键．