题目内容
5.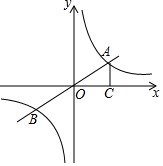 如图,直线y=kx(k为常数,k≠0)与双曲线y=$\frac{m}{x}$(m为常数,m>0)的交点为A、B,AC⊥x轴于点C,∠AOC=30°,OA=2.
如图,直线y=kx(k为常数,k≠0)与双曲线y=$\frac{m}{x}$(m为常数,m>0)的交点为A、B,AC⊥x轴于点C,∠AOC=30°,OA=2.(1)求m的值;
(2)点P在y轴上,如果S△ABP=3k,求P点的坐标.
分析 (1)求出点A坐标利用待定系数法即可解决问题;
(2)设P(0,n),由A($\sqrt{3}$,1),B(-$\sqrt{3}$,-1),可得$\frac{1}{2}$•|n|•$\sqrt{3}$+$\frac{1}{2}$•|n|•$\sqrt{3}$=3×$\frac{\sqrt{3}}{3}$,解方程即可;
解答 解:(1)在Rt△ AOC中,∵∠ACO=90°,∠AOC=30°,OA=2,
AOC中,∵∠ACO=90°,∠AOC=30°,OA=2,
∴AC=1,OC=$\sqrt{3}$,
∴A($\sqrt{3}$,1),
∵反比例函数y=$\frac{m}{x}$经过点A($\sqrt{3}$,1),
∴m=$\sqrt{3}$,
∵y=kx经过点A($\sqrt{3}$,1),
∴k=$\frac{\sqrt{3}}{3}$.
(2)设P(0,n),
∵A($\sqrt{3}$,1),B(-$\sqrt{3}$,-1),
∴$\frac{1}{2}$•|n|•$\sqrt{3}$+$\frac{1}{2}$•|n|•$\sqrt{3}$=3×$\frac{\sqrt{3}}{3}$,
∴n=±1,
∴P(0,1)或(0,-1).
点评 本题考查反比例函数与一次函数的交点问题、待定系数法,三角形的面积等知识,解题的关键是灵活应用待定系数法确定函数的解析式,学会构建方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
15.某校举办演讲比赛,对参赛20名选手的得分m(满分10分)进行分组统计,统计结果如表所示:
(1)求a的值;
(2)若用扇形图来描述,求分值在8≤m<9范围内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2,在第四组内的两名选手记为:B1、B2,现从第一组和第四组中随机选取2名选手进行座谈,用树状图或列表法列出所有可能结果,并求第一组至少有1名选手被选中的概率.
| 组号 | 分值 | 频数 |
| 一 | 6≤m<7 | 2 |
| 二 | 7≤m<8 | 8 |
| 三 | 8≤m<9 | a |
| 四 | 9≤m≤10 | 2 |
(2)若用扇形图来描述,求分值在8≤m<9范围内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2,在第四组内的两名选手记为:B1、B2,现从第一组和第四组中随机选取2名选手进行座谈,用树状图或列表法列出所有可能结果,并求第一组至少有1名选手被选中的概率.
13.下列计算正确的是( )
| A. | a8÷a4=a2 | B. | (2a2)3=6a6 | C. | 3a3-2a2=a | D. | 3a(1-a)=3a-3a2 |
17.填在下面各正方形中四个数之间都有相同的规律,根据这种规律m的值为( )


| A. | 180 | B. | 182 | C. | 184 | D. | 186 |
 小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为0.3km.
小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为0.3km.


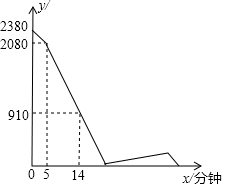 A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走.在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是180米.
A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走.在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是180米.