题目内容
18. 如图所示,热气球与水平面AB的距离CD=30米,在A处观察热气球的仰角为30°,在B处观察热气球的仰角为45°,求AB之间的距离是多少?(结果保留根号)
如图所示,热气球与水平面AB的距离CD=30米,在A处观察热气球的仰角为30°,在B处观察热气球的仰角为45°,求AB之间的距离是多少?(结果保留根号)
分析 通过解Rt△ACD和Rt△BCD分别求得AD、BD的长度,所以通过AB=AD+BD来求AB的长度即可.
解答 解:∵CD⊥AB,CD=30米,∠A=30°,
∴AD=$\frac{CD}{tan30°}$=$\frac{30}{\frac{\sqrt{3}}{3}}$=30$\sqrt{3}$(米).
又∵∠B=45°,
∴BD=$\frac{CD}{tan45°}$=$\frac{30}{1}$=30(米),
∴AB=AD+BD=(30$\sqrt{3}$+30)米.
答:AB之间的距离是(30$\sqrt{3}$+30)米.
点评 本题考查了解直角三角形的应用-仰角俯角问题.要求学生能借助仰角俯角构造直角三角形并解直角三角形,难度一般.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8. 如图,AB是⊙O直径,∠AOC=120°,则∠D=( )
如图,AB是⊙O直径,∠AOC=120°,则∠D=( )
 如图,AB是⊙O直径,∠AOC=120°,则∠D=( )
如图,AB是⊙O直径,∠AOC=120°,则∠D=( )| A. | 60° | B. | 45° | C. | 30° | D. | 20° |
9.下列说法中,正确的个数有( )
(1)减去一个数等于加上这个数;
(2)减去一个负数,差一定大于被减数;
(3)有理数的绝对值一定是正数;
(4)如果两个数的绝对值相等,那么这两个数相等.
(1)减去一个数等于加上这个数;
(2)减去一个负数,差一定大于被减数;
(3)有理数的绝对值一定是正数;
(4)如果两个数的绝对值相等,那么这两个数相等.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
6.将多项式-2x-x3+2x2+5按降幂排列,正确的是( )
| A. | x3-2x+2x2+5 | B. | 5-2x+2x2-x3 | C. | -x3+2x2+2x+5 | D. | -x3+2x2-2x+5 |
13.若关于x的一元二次方程2x2-ax+1=0的一个解是x=-1,则a的值是( )
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
3.如果a+b>0,且ab>0,那么( )
| A. | a>0,b>0 | B. | a<0,b<0 | ||
| C. | a、b异号且正数的绝对值较小 | D. | a、b异号且负数的绝对值较小 |
7.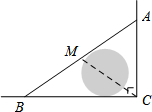 如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得BM的长为1.2km,则点M与点C之间的距离为( )
如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得BM的长为1.2km,则点M与点C之间的距离为( )
 如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得BM的长为1.2km,则点M与点C之间的距离为( )
如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得BM的长为1.2km,则点M与点C之间的距离为( )| A. | 0.5km | B. | 0.6km | C. | 0.9km | D. | 1.2km |
 如图,已知在△ABC中,AB=AC,BD是∠ABC的角平分线,且BD=BE,∠A=100°,试求∠DEC的度数.
如图,已知在△ABC中,AB=AC,BD是∠ABC的角平分线,且BD=BE,∠A=100°,试求∠DEC的度数.