题目内容
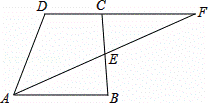
如图,已知等边△ABC,以AB为直径的半圆与BC边交于点D,过点D作⊙O的切线DF交AC于点F,过点D作DE⊥AB,垂足为点E,过点F作FG⊥AB,垂足为点G,连结GD.
(1)求证:DF⊥AC;
(2)若AB=8,求tan∠FGD的值.
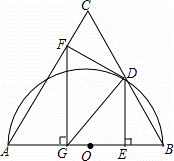
(1)证明:如图,
连接OD,
∵DF是⊙O的切线,
∴DF⊥OD.
∵△ABC为等边三角形,
∴∠A=∠B=60°,
∵OD=OB,
∴△ODB是等边三角形,
∴∠DOB=60°,
∴∠DOB=∠A,
∴OD∥AC,
∴DF⊥AC.
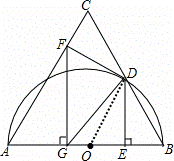
(2)解:∵FG⊥AB,DE⊥AB,
∴FG∥DE,
∴∠FGD=∠GDE,
由(1)得△OBD是等边三角形,
∴BE=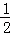 OB=
OB=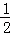 ×4=2.
×4=2.
∴DE=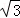 BE=2
BE=2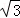 .
.
在Rt△CFD中,∠C=60°,CD=BC﹣BD=8﹣4=4,
∴CF=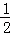 CD=2.
CD=2.
在Rt△AFG中,∠A=60°,
AF=AC﹣CF=8﹣2=6,
∴AG=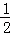 AF=3,
AF=3,
在Rt△GDE中.
GE=AB﹣AG﹣BE=8﹣3﹣2=3,
∴tan∠GDE=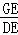 =
=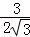 =
=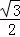 ,
,
∴tan∠FGD=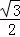 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
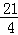 ,请求出此时①中S的值.
,请求出此时①中S的值.
 ﹣
﹣ =2.
=2.
 B.
B.  C.
C.  D.
D. 

 B.
B.  C.
C.  D.
D. 
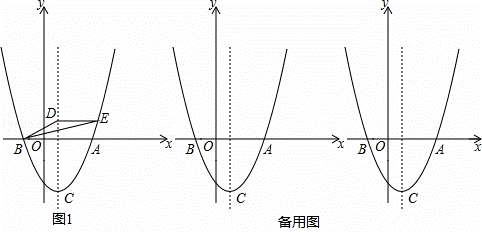
 b的图象与x轴交于A、B两点(B在A的左侧),顶点为C,点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.
b的图象与x轴交于A、B两点(B在A的左侧),顶点为C,点D(1,m)在此二次函数图象的对称轴上,过点D作y轴的垂线,交对称轴右侧的抛物线于E点.