题目内容
已知:如图,梯形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)若BC⊥AB,且BC=16,AB=17,求AF的长.
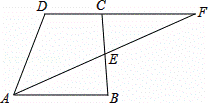
(1)证明:∵E为BC的中点
∴BE=CE
∵AB∥CD
∴∠BAE=∠F,∠B=∠FCE,
在△ABE和△FCE中,
 ,
,
∴△ABE≌△FCE(AAS);
(2)解:由(1)可得:△ABE≌△FCE,
∴CE=AB=15,CE=BE=8,AE=EF,
∵∠B=∠BCF=90°,
根据勾股定理得:AE= =17,
=17,
∴AF=34.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
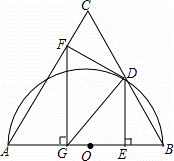
 无意义,则实数x的值是
无意义,则实数x的值是  ,求图中阴影部分图形的面积(结果保留3个有效数字)(备用数据:
,求图中阴影部分图形的面积(结果保留3个有效数字)(备用数据:

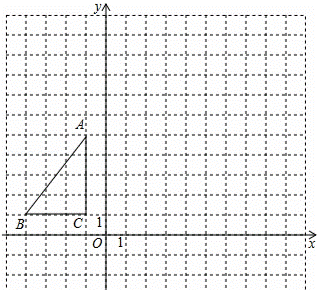
 的图象上,则k= .
的图象上,则k= .