题目内容
8.已知关于x的一元二次方程x2+mx-n=0的两个实数根为x1x2,若x1+x2=2,x1x2=-3.(1)则m=-2,n=3.
(2)求x12+x22的值.
分析 (1)根据根与系数的关系得到x1+x2=-m=2,x1x2=-n=-3.然后解方程即可;
(2)据根与系数的关系得到x1+x2=2,x1x2=-3,再利用完全平方公式得到x12+x22=(x1+x2)2-2x1x2,然后利用整体代入的方法计算.
解答 解:(1)∵方程x2+mx-n=0的两个实数根为x1x2,若x1+x2=2,x1x2=-3.
∴m=-2,n=3;
故答案为:-2,3;
(2)∵x1+x2=2,x1x2=-3,
∴x12+x22=(x1+x2)2-2x1x2=10.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
18.已知反比例函数y=$\frac{1-2m}{x}$的图象上有两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是( )
| A. | m<0 | B. | m>0 | C. | m<$\frac{1}{2}$ | D. | m>$\frac{1}{2}$ |
13.下列计算正确的是( )
| A. | a3•a2=a6 | B. | x8÷x4=x2 | C. | (a+b)(a-b)=a2+b2 | D. | (-x3y)2=x6y2 |
18.记录一天中气温的变化情况,选用比较合适的统计图是( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 以上三种都可以 |

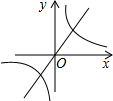
 已知一次函数y=kx+b的图象(如图所示),那么正比例函数y=kx和反比例函数y=$\frac{b}{x}$在同一坐标系的图象可能是( )
已知一次函数y=kx+b的图象(如图所示),那么正比例函数y=kx和反比例函数y=$\frac{b}{x}$在同一坐标系的图象可能是( )