题目内容
19.已知函数y1=kx-2和y2=3x+b相交于点A(2,-1).(1)求k、b的值,在同一坐标系中画出两个函数的图象.
(2)利用图象求出:当x取何值时有:①y1>y2;②y1≤y2.
分析 (1)将点A(2,-1)代入函数的解析式可求得k,b的值,然后可画出两函数的图象;
(2)根据函数图象和交点A的坐标即可求得.
解答  解:(1)将A点坐标代入y1,得:2k-2=-1,即k=$\frac{1}{2}$;
解:(1)将A点坐标代入y1,得:2k-2=-1,即k=$\frac{1}{2}$;
将A点坐标代入y2,得:-6+b=-1,即b=5;
∴两个函数的解析式分别为:y1=$\frac{1}{2}$x-2、y2=-3x+5;如图;
(2)从图象可以看出:①当x>2时,y1>y2;②当x≤2时,
y1≤y2.
点评 本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.

练习册系列答案
相关题目
7.Rt△ABC中,∠C=90°,如果各边的长度都扩大到原来的2倍,那么sinA的值( )
| A. | 都扩大到原来的2倍 | B. | 都缩小到原来的一半 | ||
| C. | 没有变化 | D. | 不能确定 |
9.当x=-2时,2x3+2x2-ax-8=0,则当x=2时,2x3+2x2-ax-8的值为( )
| A. | 0 | B. | -2 | C. | -4 | D. | -8 |
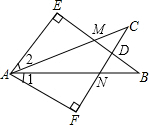 己知如图,∠E=∠F=90°,∠B=∠C,AE=AF.
己知如图,∠E=∠F=90°,∠B=∠C,AE=AF.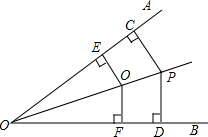 如图,PC⊥OA于点C,PD⊥OB于点D,PC=PD,Q是OP上一点,QE⊥OA于点E,QF⊥OB于点F,求证:QE=QF.
如图,PC⊥OA于点C,PD⊥OB于点D,PC=PD,Q是OP上一点,QE⊥OA于点E,QF⊥OB于点F,求证:QE=QF.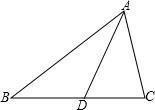 如图,△ABC中,∠BAC=54°,∠B=46°,AD是∠BAC的角平分线,求∠ADC、∠ADB的度数.
如图,△ABC中,∠BAC=54°,∠B=46°,AD是∠BAC的角平分线,求∠ADC、∠ADB的度数. 如图,在△ABC中,AB=AC=8cm,∠BAC=40°,以腰AB为直径作半圆O,分别交BC,AC于点D,E.求$\widehat{BD}$,$\widehat{AE}$的长.
如图,在△ABC中,AB=AC=8cm,∠BAC=40°,以腰AB为直径作半圆O,分别交BC,AC于点D,E.求$\widehat{BD}$,$\widehat{AE}$的长.