题目内容
19.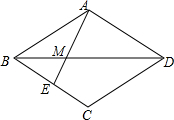 如图,在菱形ABCD中,E在BC上,AE交BD于点M,AB=AE,2∠BAE=∠EAD.求证:BE=BM.
如图,在菱形ABCD中,E在BC上,AE交BD于点M,AB=AE,2∠BAE=∠EAD.求证:BE=BM.
分析 设∠BAE=x,然后根据等腰三角形两底角相等表示出∠ABE,再根据菱形的邻角互补求出∠ABE,根据三角形内角和定理列出方程,求出x的值,求出∠BME和∠BEM的度数,即可得出答案.
解答 证明:∵四边形ABCD是菱形,
∴AD∥BC,
∴∠ABE+∠BAE+∠EAD=180°,
设∠BAE=x°,
则∠EAD=2x°,∠ABE=180°-x°-2x°,
∵AB=AE,∠BAE=x°,
∴∠ABE=∠AEB=180°-x°-2x°,
由三角形内角和定理得:x+180-x-2x+180-x-2x=180,
解得:x=36,
即∠BAE=36°,
∠BAE=180°-36°-2×36°=70°,
∵四边形ABCD是菱形,
∴∠BAD=∠CBD=$\frac{1}{2}$∠ABE=36°,
∴∠BME=∠ABD+∠BAE=36°+36°=72°,
∴∠BEM=180°-36°-72°=72°,
∴BE=BM.
点评 本题考查了菱形的性质,等腰三角形的性质,熟记各性质并列出关于∠BAE的方程是解题的关键,注意:菱形的对边平行,菱形的对角线平分一组对角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列的计算正确的是( )
| A. | a(a-1)=a2-1 | B. | (x-2)(x+4)=x2-8 | C. | (x+2)2=x2+4 | D. | (x-2)(x+2)=x2-4 |
9.已知二次函数y=x2+x+c的图象与x轴的一个交点为(2,0),则它与x轴的另一个交点坐标是( )
| A. | (1,0) | B. | (-1,0) | C. | (2,0) | D. | (-3,0) |
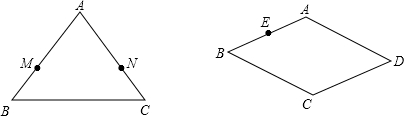
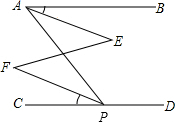 如图,∠BAP+∠APD=180°,∠BAE=∠CPF,求证:AE∥PF.
如图,∠BAP+∠APD=180°,∠BAE=∠CPF,求证:AE∥PF.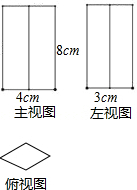 一个直四棱柱的三视图如图所示,俯视图是一个菱形,求这个直四棱柱的表面积.
一个直四棱柱的三视图如图所示,俯视图是一个菱形,求这个直四棱柱的表面积.