题目内容
9.一个菱形的周长为52cm,一条对角线长为10cm,则其面积为120cm2.分析 先由菱形ABCD的周长求出边长,再根据菱形的性质求出OA,然后由勾股定理求出OB,即可得出BD,再根据菱形的面积等于对角线乘积的一半计算即可.
解答 解:如图所示: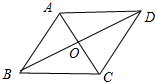 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AC⊥BD,OA=$\frac{1}{2}$AC=5,OB=$\frac{1}{2}$BD,
∵菱形ABCD的周长为52cm,
∴AB=13cm,
在Rt△AOB中,根据勾股定理得:OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12cm,
∴BD=2OB=24cm,
∴菱形ABCD的面积=$\frac{1}{2}$×10×24=120cm2,
故答案为120.
点评 本题考查了菱形的性质以及勾股定理的运用;熟练掌握菱形的性质和运用勾股定理计算是解决问题的关键.

练习册系列答案
相关题目
19.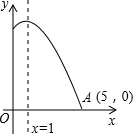 如图,二次函数y=ax2+bx+c的图象的一部分过点A(5,0),对称轴为直线x=1,则下列结论中错误的是( )
如图,二次函数y=ax2+bx+c的图象的一部分过点A(5,0),对称轴为直线x=1,则下列结论中错误的是( )
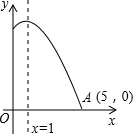 如图,二次函数y=ax2+bx+c的图象的一部分过点A(5,0),对称轴为直线x=1,则下列结论中错误的是( )
如图,二次函数y=ax2+bx+c的图象的一部分过点A(5,0),对称轴为直线x=1,则下列结论中错误的是( )| A. | abc<0 | B. | 当x<1时,y随x的增大而增大 | ||
| C. | 4a-2b+c<0 | D. | 方程ax2+bx+c=0的根为x1=-3,x2=5 |
17.经统计,2016年除夕夜观看春晚直播的观众约达10.3亿人,用科学记数法表示10.3亿正确的是( )
| A. | 1.03×109 | B. | 1.03×1010 | C. | 10.3×109 | D. | 103×108 |
4.不等式组$\left\{\begin{array}{l}{x+2≥1}\\{x-3<-1}\end{array}\right.$中的两个不等式的解集在同一个数轴上表示正确的是( )
| A. | 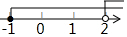 | B. | 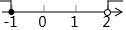 | C. | 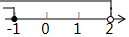 | D. |  |
14.关于$\sqrt{18}$的叙述错误的是( )
| A. | 它是一个无限不循环小数 | B. | 它在3和4之间 | ||
| C. | 它化简后为3$\sqrt{2}$ | D. | 以它为直径的圆的面积是$\frac{9}{2}$π |
19.在下列的四个几何体中,其主视图与俯视图相同的是( )
| A. |  圆柱 | B. |  圆锥 | C. |  三棱柱 | D. |  球 |
 如图,用一个半径为30cm,面积为150πcm2的扇形铁皮,制作一个无底的圆锥(不计耗损),则圆锥的底面半径r为5cm.
如图,用一个半径为30cm,面积为150πcm2的扇形铁皮,制作一个无底的圆锥(不计耗损),则圆锥的底面半径r为5cm.