题目内容
填空:
(1)(m-2n)2- =(m+2n)2;
(2)若(x-a)(x-3)=x2-x+b,则a= ,b= ;
(3)若2x2-3x-1=0,则6x2-9x-5= ;
(4)(12a2b6-4a7b5)÷ =6b4-2a5b3;
(5)(x-2y+1)(x+2y-1)= ;
(6)(2x-3y)(-3y-2x)= ;
(7)(
x-
y)• =
y2-
x2;
(8)(-x+y)2= .
(1)(m-2n)2-
(2)若(x-a)(x-3)=x2-x+b,则a=
(3)若2x2-3x-1=0,则6x2-9x-5=
(4)(12a2b6-4a7b5)÷
(5)(x-2y+1)(x+2y-1)=
(6)(2x-3y)(-3y-2x)=
(7)(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 4 |
(8)(-x+y)2=
考点:整式的混合运算
专题:计算题
分析:(1)原式利用完全平方公式计算即可;
(2)已知等式左边利用多项式乘以多项式法则计算,利用多项式相等的条件求出a与b的值即可;
(3)已知等式变形求出2x2-3x的值,原式变形后代入计算即可求出值;
(4)原式利用多项式除以单项式法则计算即可;
(5)原式利用平方差公式及完全平方公式计算即可;
(6)原式利用平方差公式计算即可;
(7)原式利用平方差公式计算即可;
(8)原式利用完全平方公式展开即可.
(2)已知等式左边利用多项式乘以多项式法则计算,利用多项式相等的条件求出a与b的值即可;
(3)已知等式变形求出2x2-3x的值,原式变形后代入计算即可求出值;
(4)原式利用多项式除以单项式法则计算即可;
(5)原式利用平方差公式及完全平方公式计算即可;
(6)原式利用平方差公式计算即可;
(7)原式利用平方差公式计算即可;
(8)原式利用完全平方公式展开即可.
解答:解:(1)(m-2n)2-(-8mn)=(m+2n)2;
(2)若(x-a)(x-3)=x2-x+b,则a=-2,b=-6;
(3)若2x2-3x-1=0,则6x2-9x-5=-2;
(4)(12a2b6-4a7b5)÷2a2b2=6b4-2a5b3;
(5)(x-2y+1)(x+2y-1)=x2-(2y-1)2=x2-4y2+4y-1;
(6)(2x-3y)(-3y-2x)=9y2-4x2;
(7)(
x-
y)•(-
x-
y)=
y2-
x2;
(8)(-x+y)2=x2-2xy+y2.
故答案为:(1)-8mn;(2)-2;-6;(3)-2;(4)2a2b2;(5)x2-4y2+4y-1;(6)9y2-4x2;(7)(-
x-
y);(8)x2-2xy+y2
(2)若(x-a)(x-3)=x2-x+b,则a=-2,b=-6;
(3)若2x2-3x-1=0,则6x2-9x-5=-2;
(4)(12a2b6-4a7b5)÷2a2b2=6b4-2a5b3;
(5)(x-2y+1)(x+2y-1)=x2-(2y-1)2=x2-4y2+4y-1;
(6)(2x-3y)(-3y-2x)=9y2-4x2;
(7)(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 4 |
(8)(-x+y)2=x2-2xy+y2.
故答案为:(1)-8mn;(2)-2;-6;(3)-2;(4)2a2b2;(5)x2-4y2+4y-1;(6)9y2-4x2;(7)(-
| 1 |
| 2 |
| 1 |
| 3 |
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
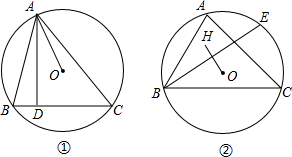 如图①,小聪在学习圆的性质时发现一个结论,△ABC内接于⊙O,AD⊥BC,则∠BAD=∠OAC.
如图①,小聪在学习圆的性质时发现一个结论,△ABC内接于⊙O,AD⊥BC,则∠BAD=∠OAC.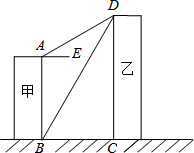 如图,线段AB、CD分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,AE∥BC,测得∠DBC=60°,∠DAE=30°,已知甲建筑物高AB=36米.求乙建筑物的高CD.
如图,线段AB、CD分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,AE∥BC,测得∠DBC=60°,∠DAE=30°,已知甲建筑物高AB=36米.求乙建筑物的高CD. 如图,在⊙O中,CD为直径,AB为弦,且CD平分AB于E,OE=3cm,AB=8cm.
如图,在⊙O中,CD为直径,AB为弦,且CD平分AB于E,OE=3cm,AB=8cm.