题目内容
12.当x=2时,抛物线y=ax2+bx+c取得最小值为-3,且抛物线与y轴交于点C(0,1).(1)求该抛物线对应的函数表达式;
(2)若点M(m,y1),N(m+2,y2)都在抛物线上,试比较y1与y2的大小.
分析 (1)已知,当x=2时,抛物线的最小值为-3,因此抛物线的顶点坐标为(2,-3);可用顶点式来设抛物线的解析式,然后将C的坐标代入即可求出抛物线的解析式.
(2)可先将M,N的坐标代入(1)的抛物线解析式中,可得出y1、y2的表达式.然后让y1-y2,然后看得出的结果中在x的不同取值范围下,y1、y2的大小关系.
解答 解:(1)由题意可设抛物线的关系式为:
y=a(x-2)2-3,
因为点C(0,1)在抛物线上,
所以1=a(0-2)2-3,即a=1,
所以,抛物线的关系式为y=(x-2)2-3=x2-4x+1;
(2)∵点M(m,y1),N(m+2,y2)都在该抛物线上,
∴y1-y2=(m2-4m+1)-[(m+2)2-4(m+2)+1]=4-4m,
当4-4m>0,即m<1时,y1>y2,
当4-4m=0,即m=1时,y1=y2,
当4-4m<0,即m>1时,y1<y2.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数图象上点的坐标特征.

练习册系列答案
相关题目
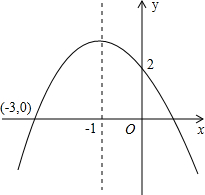 已知抛物线的图象如图所示,求这个抛物线的解析式.
已知抛物线的图象如图所示,求这个抛物线的解析式.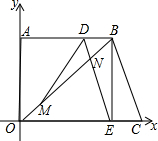 如图,在直角梯形OABC中,已知B、C两点的坐标分别为B(8,6)、C(10,0),动点M由原点O出发沿OB方向匀速运动,速度为1单位/秒;同时,线段DE由BC出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM,设运动时间为t秒(0<t<8)
如图,在直角梯形OABC中,已知B、C两点的坐标分别为B(8,6)、C(10,0),动点M由原点O出发沿OB方向匀速运动,速度为1单位/秒;同时,线段DE由BC出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM,设运动时间为t秒(0<t<8)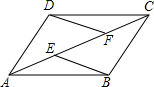 如图,AB=DC,DF=BE,AF=CE,求证:
如图,AB=DC,DF=BE,AF=CE,求证: