题目内容
6. (1)操作发现 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
(1)操作发现 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.(2)问题解决 保持(1)中的条件不变,若DC=3DF,求$\frac{AD}{AB}$的值;
(3)类比探求 保持(1)中条件不变,若DC=mDF,求$\frac{AD}{AB}$的值.
分析 (1)求简单的线段相等,可证线段所在的三角形全等,即连接EF,证△EGF≌△EDF即可;
(2)可设DF=x,BC=y;进而可用x表示出DC、AB的长,根据折叠的性质知AB=BG,即可得到BG的表达式,由(1)证得GF=DF,那么GF=x,由此可求出BF的表达式,进而可在Rt△BFC中,根据勾股定理求出x、y的比例关系,即可得到$\frac{AD}{AB}$的值;
(3)仿照(2)的方法得出答案即可.
解答 解:(1)同意,连接EF,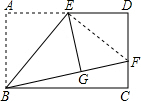 则根据翻折不变性得,
则根据翻折不变性得,
∠EGF=∠D=90°,EG=AE=ED,EF=EF,
在Rt△EGF和Rt△EDF中,
$\left\{\begin{array}{l}{EG=ED}\\{EF=EF}\end{array}\right.$,
∴Rt△EGF≌Rt△EDF(HL),
∴GF=DF;
(2)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=3DF,
∴CF=2x,DC=AB=BG=3x,
∴BF=BG+GF=4x;
在Rt△BCF中,BC2+CF2=BF2,即y2+(2x)2=(4x)2
∴y=2$\sqrt{3}$x,
∴$\frac{AD}{AB}$=$\frac{2\sqrt{3}x}{3x}$=$\frac{2\sqrt{3}}{3}$;
(3)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=m•DF,
∴BF=BG+GF=(m+1)x
在Rt△BCF中,BC2+CF2=BF2,即y2+[(m-1)x]2=[(m+1)x]2
∴y=2x$\sqrt{m}$,
∴$\frac{AD}{AB}$=$\frac{2x\sqrt{m}}{mx}$=$\frac{2\sqrt{m}}{m}$.
点评 此题考查了折叠变换,全等三角形的判定和性质,勾股定理的应用,灵活表示每条线段的长度是解决问题的关键.

 为了让广大青少年学生走向操场,走进自然,走到阳光下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”.小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.
为了让广大青少年学生走向操场,走进自然,走到阳光下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”.小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.(1)请根据图中信息,补全下面的表格;
| 次数 | 1 | 2 | 3 | 4 | 5 |
| 小明 | 13.3 | 13.4 | 13.3 | 13.2 | 13.3 |
| 小亮 | 13.2 | 13.4 | 13.1 | 13.5 | 13.3 |
(3)分别计算他们的平均数、极差和方差填入右表格,若你是他们的教练,将小明与小亮的成绩比较后,你将分别给予他们怎样的建议?
| 平均数 | 极差 | 方差 | |
| 小明 | 13.3 | 0.2 | 0.004 |
| 小亮 | 13.3 | 0.4 | 0.02 |
 一元一次方程$\frac{1}{2}$x-1=2的解表示在数轴上,是图中数轴上的哪个点( )
一元一次方程$\frac{1}{2}$x-1=2的解表示在数轴上,是图中数轴上的哪个点( )| A. | D点 | B. | C点 | C. | B点 | D. | A点 |

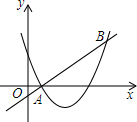 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2),不等式x2+bx+c<x+m的解集为1<x<3.
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2),不等式x2+bx+c<x+m的解集为1<x<3.