题目内容
4.为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,某校随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图如图,请根据统计图中的信息回答下列问题: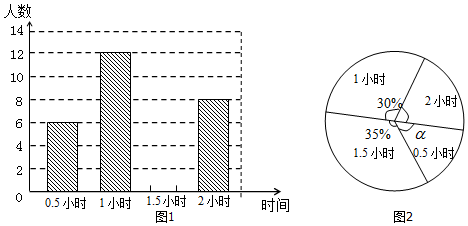
(1)此次抽样调查中,共调查了多少名学生?
(2)将图1补充完整;
(3)求出图2中圆心角α的度数;
(4)请估算该校九年级学生自主学习时间不少于1.5小时的有多少人?
分析 (1)根据1小时的人数和所占的百分比,即可求出总人数;
(2)用1.5小时的人数所占的百分比乘以抽查的人数即可求出1.5小时的人数,从而补全统计图;
(3)用0.5小时的人数除以抽查的人数,再乘以360度,即可求出圆心角α的度数;
(4)用总人数乘以该校九年级学生自主学习时间不少于1.5小时所占的百分比,即可求出该校九年级学生自主学习时间不少于1.5小时的人数.
解答  解:(1)12÷30%=40人,
解:(1)12÷30%=40人,
答:共调查了40名学生;
(2)自主学习时间等于1.5小时的有40×35%=14人;
如图所示,
(3)圆心角α的度数是360°×$\frac{6}{40}$=54°;
(4)该校九年级学生自主学习时间不少于1.5小时的有多少人600×$\frac{14+8}{40}$=330人.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
15.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | (-3)2=6 | C. | (-a3)2=a6 | D. | a2+a3=a5 |
13.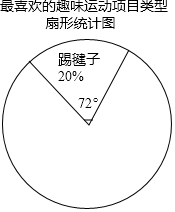 某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
(1)直接写出a=0.25,b=40;
(2)利用频数分布表中的数据,在图中绘制扇形统计图(注明项目、百分比、圆心角);
(3)若全校共有学生1200名,估计该校最喜爱背夹球和拔河的学生大约有多少人?
 某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
| 项目类型 | 频数 | 频率 |
| 跳长绳 | 25 | a |
| 踢毽子 | 20 | 0.2 |
| 背夹球 | b | 0.4 |
| 拔河 | 15 | 0.15 |
(2)利用频数分布表中的数据,在图中绘制扇形统计图(注明项目、百分比、圆心角);
(3)若全校共有学生1200名,估计该校最喜爱背夹球和拔河的学生大约有多少人?
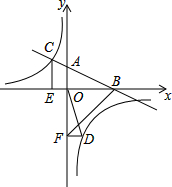 如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第二象限交于点C,CE⊥x轴,垂足为点E,sin∠ABO=$\frac{\sqrt{5}}{5}$,OB=2,OE=1.
如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第二象限交于点C,CE⊥x轴,垂足为点E,sin∠ABO=$\frac{\sqrt{5}}{5}$,OB=2,OE=1.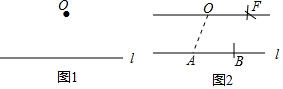 下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.
下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.