题目内容
4.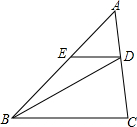 如图,DE∥BC,S△ADE=3,S△CBD=18,求S△ABC.
如图,DE∥BC,S△ADE=3,S△CBD=18,求S△ABC.
分析 由DE∥BC可得△ADE∽△ACB,从而可知两三角形面积的关系;△BED与△ADE为同底三角形,则可求出面积的关系,结合S△ABC=S△ADE+S△BDE+S△CBD即可求得答案.
解答 解:∵DE∥BC,
∴△ADE∽△ACB,
设$\frac{AB}{AE}$=k,
则S△ABC=3k2,
由相似三角形对应边的比可知△BED的边DE的高:△ADE的边DE的高=k-1:1,
∴S△BDE=3(k-1),
∵S△ABC=S△ADE+S△BDE+S△CBD,
∴3k2=3+3(k-1)+18,
解得k1=3,k2=-2(舍去),
∴S△ABC=27.
点评 本题考查了相似三角形的判定和性质,同底三角形的面积关系,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.在Rt△ABC和Rt△A′B′C′,∠C=∠C′=90°,AC=A′C′,AB=A′B′,下列结论错误的是( )
| A. | ∠A=∠A′ | B. | BC=B′C′ | C. | AC=B′C′ | D. | ∠B=∠B′ |

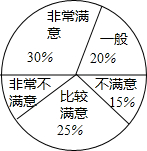 如图是市民对“净畅宁工程”满意程度的扇形统计图.回答下列问题.
如图是市民对“净畅宁工程”满意程度的扇形统计图.回答下列问题.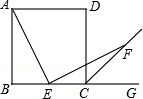 如图,四边形ABCD是正方形,点E在BC上,AE⊥EF,CF是∠DCG的平分线.
如图,四边形ABCD是正方形,点E在BC上,AE⊥EF,CF是∠DCG的平分线.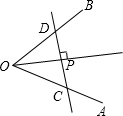 如图所示,OP平分∠AOB,过点P作OP的垂线分别交OA,OB于点C,D,问PC=PD吗?为什么?
如图所示,OP平分∠AOB,过点P作OP的垂线分别交OA,OB于点C,D,问PC=PD吗?为什么?