题目内容
12.如图,在菱形ABCD中,把∠A、∠C分别翻折,使点A、C分别落在对角线BD上的点H、G处,折痕分别是DF、BE.(1)求证:△ADF≌△CBE;
(2)如图2,连接GF、EH,求证四边形EHFG是平行四边形;
(3)如图3,在图2的基础上连接EF,交BD于点O,将∠A=120°,AD=4,求证∠FOB=45°,求线段EF的长.

分析 (1)先由菱形的性质和折叠的性质得到全等三角形的条件;
(2)由折叠和菱形的对称性得出EG=FH,再判断出FH∥EG即可;
(3)过点F作FM⊥BD,设出HM,利用含30°的直角三角形的性质表示出FM,FH,FB,OB,判断出FM=OM即可.
解答 解:(1)∵BD是菱形ABCD对角线,
∴∠ADB=∠CBD,AD=BC,∠A=∠C
由折叠知,∠ADF=$\frac{1}{2}$∠ABD,∠CBE=$\frac{1}{2}$∠CBE,
∴∠ADF=∠CBE,
在△ADF和△CBE中$\left\{\begin{array}{l}{∠ADF=∠CBE}\\{AD=BC}\\{∠A=∠C}\end{array}\right.$,
∴△ADF≌△CBE,
(2)由折叠得,AF=FH=CE=EG,∠FHD=∠A=∠C=∠EGB,
∴FH∥EG,
∴四边形EHFG是平行四边形;
(3)①如图3,设HM=a,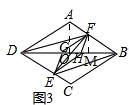 由折叠知,∠FHD=120°,
由折叠知,∠FHD=120°,
∴∠FHM=60°,
∴∠HFM=30°,
∴FM=$\sqrt{3}$a,FH=2a,
∵∠FMB=90°,
∴BM=3a
∵∠ABD=30°,∠FHB=60°,
∴∠BFH=90°,
∴BF=2$\sqrt{3}$a,
∴AB=AF+BF=FH+BF=2($\sqrt{3}$+1)a,
∵∠AOB=90°,∠ABO=30°,
∴OB=(3+$\sqrt{3}$)a,
∴OM=OB-BM=$\sqrt{3}$a,
∴FM=OM,
∵∠FMO=90°,
∴∠FOB=45°,
②∵∠FMO=90°,∠FOB=45°,
∴OF=$\sqrt{2}$OM=$\sqrt{6}$a,
∵AD=4,
∴2($\sqrt{3}$+1)a=4,
∴a=$\frac{3}{\sqrt{3}+1}$
∴EF=2OF=2$\sqrt{6}$×$\frac{2}{\sqrt{3}+1}$=6$\sqrt{2}$-2$\sqrt{6}$.
点评 此题是四边形综合题,主要考查了菱形的性质,折叠的性质,全等三角形的判定和性质,含30°的直角三角形的性质,勾股定理,解本题的关键是判断出四边形EHFG是平行四边形,作出辅助线,用代数的方法得出FM=OM是解本题的难点.

| A. | 70° | B. | 90° | C. | 110° | D. | 140° |
| A. | $\frac{1}{10}$ | B. | $\frac{7}{4}$ | C. | $-\frac{1}{5}$ | D. | -1 |
| A. | -9 | B. | 1 | C. | -1 | D. | 9 |
 如图,正方形BODC的顶点C的坐标是(3,3),以原点O为位似中心,将正方形BODC缩小后得到正方形B'ODC',点C的对应点C'的坐标为(-1,-1),那么点D的对应点D'的坐标为( )
如图,正方形BODC的顶点C的坐标是(3,3),以原点O为位似中心,将正方形BODC缩小后得到正方形B'ODC',点C的对应点C'的坐标为(-1,-1),那么点D的对应点D'的坐标为( )| A. | (-1,0) | B. | (0,-1) | C. | (1,0) | D. | (0,1) |
| A. | 76 | B. | 74 | C. | 75 | D. | 81 |
 如图,AB∥CD,EF交CD于点H,EG⊥AB,垂足为G,已知∠CHE=120°,则∠FEG=30°.
如图,AB∥CD,EF交CD于点H,EG⊥AB,垂足为G,已知∠CHE=120°,则∠FEG=30°.