题目内容
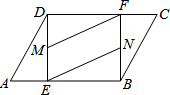 如图,?ABCD中,E、F分别是AB、CD上的点,且AE=CF,M、N分别为DE、BF的中点,连结MF、NE,求证:MF∥EN.
如图,?ABCD中,E、F分别是AB、CD上的点,且AE=CF,M、N分别为DE、BF的中点,连结MF、NE,求证:MF∥EN.考点:平行四边形的判定与性质
专题:证明题
分析:由四边形ABCD为平行四边形,利用平行四边形的对边平行且相等得到CD平行且相等于AB,再由AE=CF,得到DF与BE平行且相等,得到四边形DEBF为平行四边形,进而得到DE与BF平行且相等,根据M、N分别为DE、BF的中点,得到ME与FN平行且相等,确定出四边形MENF为平行四边形,利用平行四边形的对边平行即可得证.
解答:证明:∵四边形ABCD为平行四边形,
∴CD∥AB,CD=AB,
∵AE=CF,
∴CD-CF=AB-AE,即DF=EB,
∴四边形DEBF为平行四边形,
∴DE∥BF,DE=BF,
∵M、N分别为DE、BF的中点,
∴ME=FN=
DE=
BF,
∴四边形MENF为平行四边形,
则MF∥EN.
∴CD∥AB,CD=AB,
∵AE=CF,
∴CD-CF=AB-AE,即DF=EB,
∴四边形DEBF为平行四边形,
∴DE∥BF,DE=BF,
∵M、N分别为DE、BF的中点,
∴ME=FN=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形MENF为平行四边形,
则MF∥EN.
点评:此题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目