题目内容
10. 如图,在Rt△ABC中,∠ACB=90°,△ABC绕点A旋转得到△ADE(E与C对应,D与B对应),连接EC并延长交BD于F.
如图,在Rt△ABC中,∠ACB=90°,△ABC绕点A旋转得到△ADE(E与C对应,D与B对应),连接EC并延长交BD于F.(1)求证:∠DEF=∠BCF;
(2)求证:BF=DF;
(3)当AC=BC时,连接BE,若△BCE的面积等于2,求BD的长?
分析 (1)如图1,由旋转得对应边相等,对应角相等,则AC=AE,∠ACB=∠AED=90°,利用等角的余角相等得结论;
(2)如图2,作辅助线,构建两个全等三角形,证明△EDF≌△CBN,再利用等角对等边和等量代换得:BF=DF;
(3)如图3,作辅助线,构建三角形的高线,利用三角形全等得EF=CN,则EC=FN,所以△ECB和△FBN是等底同高的两个三角形面积相等,设FM=x,根据△BCE的面积等于2列式求出x的值,则DB=4.
解答 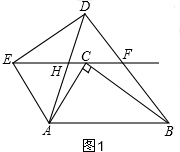 证明:(1)如图1,由旋转得:AC=AE,∠ACB=∠AED=90°,
证明:(1)如图1,由旋转得:AC=AE,∠ACB=∠AED=90°,
∴∠CEA=∠ECA,
∴∠DEF+∠AEC=90°,∠ECA+∠BCF=90°,
∴∠DEF=∠BCF;
(2)如图2,作∠CBN=∠EDF,交EF延长线于点N,
∵DE=BC,∠DEF=∠BCF,
∴△EDF≌△CBN,
∴DF=BN,∠DFE=∠N,
∵∠DFE=∠BFN,
∴∠BFN=∠N,
∴BF=BN,
∴BF=DF;
(3)如图3,作∠CBN=∠EDF,交EF延长线于点N,过B作BM⊥EN于M,连接AF,
由(2)得:△EDF≌△CBN,
∴EF=CN,
∴EF-CF=CN-CF,
即EC=FN,
∵AD=AB,DF=BF,
∴AF⊥BD,
∴∠AFB=90°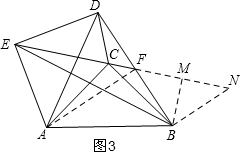 ,
,
∵∠ACB=90°,
∴A、C、F、B四点共圆,
∴∠CFA=∠CBA=45°,
∴∠BFN=180°-90°-45°=45°,
∴△FMB是等腰直角三角形,
设FM=x,则BM=FM=MN=x,
∵S△ECB=$\frac{1}{2}$EC•BM,
S△BFN=$\frac{1}{2}$FN•BM,
∴S△ECB=S△BFN,
∵S△ECB=2,
∴$\frac{1}{2}$•2x•x=2,
x=±$\sqrt{2}$,
∴FM=$\sqrt{2}$,
∴BF=$\sqrt{2}$FM=2,
∴BD=2BF=4.
点评 本题是三角形的综合题,也是旋转变换问题,首先明确旋转前后的两个三角形对应边相等,对应角相等;巧妙地做一个角等于已知角,构建两个三角形全等,根据对应边相等与等角对等边相结合得出结论;本题还利用了四点共圆证明两角相等,等腰直角三角形的锐角是45°和斜边是直角边的$\sqrt{2}$倍,以及利用三角形面积公式求出边的长度.

 在甲组图形的四个图中,每个图是由四种图形A,B,C,D(不同的线段或圆)中的某两个图形组成的,例如由A,B组成的图形记为A*B,在乙组图形的(a),(b),(c),(d)四个图形中,表示“A*D”和“A*C”的是( )
在甲组图形的四个图中,每个图是由四种图形A,B,C,D(不同的线段或圆)中的某两个图形组成的,例如由A,B组成的图形记为A*B,在乙组图形的(a),(b),(c),(d)四个图形中,表示“A*D”和“A*C”的是( )| A. | (a),(b) | B. | (b),(c) | C. | (c),(d) | D. | (b),(d) |
 如图,在四边形ABCD中,AC与BD交于点M,若∠ADM=40°,∠AMD=90°,AB=AC=AD,则∠ABC的度数为( )
如图,在四边形ABCD中,AC与BD交于点M,若∠ADM=40°,∠AMD=90°,AB=AC=AD,则∠ABC的度数为( )| A. | 55° | B. | 60° | C. | 65° | D. | 75° |
| A. | 有一个角对应相等的两个直角三角形相似 | |
| B. | 如果两个图形位似,那么对应线段平行或在同一条直线直线上 | |
| C. | 两个矩形一定相似 | |
| D. | 如果将一个三角形的各边长都扩大二倍,则其面积将扩大4倍 |

