题目内容
14. 如图,点D为线段AB延长线上一点,△ABC和△BDE分别是以AB,BD为斜边的等腰直角三角形.连接CE并延长,交AD的延长线于F,△ABC的外接圆圆O交CF与点M.若AB=6,BD=2.
如图,点D为线段AB延长线上一点,△ABC和△BDE分别是以AB,BD为斜边的等腰直角三角形.连接CE并延长,交AD的延长线于F,△ABC的外接圆圆O交CF与点M.若AB=6,BD=2.(1)求CE长度;
(2)证明:AC2=CM•CF;
(3)求CM长度.
分析 (1)由△ABC和△BDE等腰直角三角形,AB=6,BD=2.得到BC=$\frac{\sqrt{2}}{2}$AB=3$\sqrt{2}$,BE=$\frac{\sqrt{2}}{2}$BD=$\sqrt{2}$,∠ABC=∠EBD=45°,∠CBE=90°,根据勾股定理即可求得CE=$\sqrt{{CB}^{2}{+BE}^{2}}$=2$\sqrt{5}$;
(2)欲证AC2=CM•CF,即证AC:CF=CM:AC,连接AM,通过证明△ACM∽△FCA可以得出;
(3)根据△EDF∽△CBF,得到$\frac{DF}{BF}$=$\frac{DE}{BC}$=$\frac{EF}{CF}$,$\frac{EF}{EF+CE}$=$\frac{DF}{BD+DF}$=$\frac{\sqrt{2}}{3\sqrt{2}}$=$\frac{1}{3}$,求出BF=3,CF=3$\sqrt{5}$,根据切割线定理得到BF•AF=FM•CF,求出FM=$\frac{9\sqrt{5}}{5}$,即可得CM=3$\sqrt{5}$-$\frac{9\sqrt{5}}{5}$=$\frac{6\sqrt{5}}{5}$.
解答 解:(1)∵△ABC和△BDE等腰直角三角形,AB=6,BD=2.
∴BC=$\frac{\sqrt{2}}{2}$AB=3$\sqrt{2}$,BE=$\frac{\sqrt{2}}{2}$BD=$\sqrt{2}$,∠ABC=∠EBD=45°,
∴∠CBE=90°,
∴CE=$\sqrt{{CB}^{2}{+BE}^{2}}$=2$\sqrt{5}$;
(2)证明:连接AM,则∠AMC=∠ABC=∠CAF=45°,
∵∠ACM=∠FCA
∴△ACM∽△FCA,
∴$\frac{AC}{CF}$=$\frac{CM}{AC}$,
∴AC2=CM•CF;
(3)∵∠ABC=∠BDE,
∴DE∥BC,
∴△EDF∽△CBF,
∴$\frac{DF}{BF}$=$\frac{DE}{BC}$=$\frac{EF}{CF}$,
∴$\frac{EF}{EF+CE}$=$\frac{DF}{BD+DF}$=$\frac{\sqrt{2}}{3\sqrt{2}}$=$\frac{1}{3}$,
∴BF=3,CF=3$\sqrt{5}$,
∵BF•AF=FM•CF,
∴FM=$\frac{9\sqrt{5}}{5}$,
∴CM=3$\sqrt{5}$-$\frac{9\sqrt{5}}{5}$=$\frac{6\sqrt{5}}{5}$.
点评 本题考查了切线的判定及有关性质,相似三角形的判定和性质,综合性较强,有一定的难度.

| A. | 3a-b | B. | 3(x-y) | C. | x-y | D. | 3a+b |
| A. | a0=1 | B. | 夹在两条平行线间的线段相等 | ||
| C. | 若$\frac{\sqrt{x-1}}{x-2}$有意义,则x≥1且x≠2 | D. | 勾股定理是a2+b2=c2 |
| A. | $\sqrt{\frac{1}{2}x}$ | B. | $\sqrt{18x}$ | C. | $\sqrt{3x}$ | D. | $\sqrt{{x}^{2}y}$ |
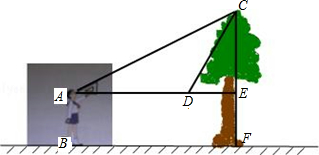 如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高AB为1.7m,求这棵树的高度.(结果精确到0.1m,$\sqrt{3}$≈1.73)
如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高AB为1.7m,求这棵树的高度.(结果精确到0.1m,$\sqrt{3}$≈1.73) 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究: