Question

△ABC中∠B=90°，以B为圆心，AB为半径的⊙B交斜边AC于D，E为BC上一点使得DE=CE．
（1）证明：DE为⊙B的切线；
（2）若BC=8、DE=3，求线段AC的长．

Answer 1

（1）证明：连BD，得∠C=∠CDE，
∠A=∠ADB，而∠A+∠C=90°．
所以∠CDE+∠ADB=90°即BD⊥DE．
所以DE为切线．

（2）解：∵CE=DE=3，BC=8，
∴BE=5．
在Rt△BDE中，BD==4，
∴Rt△ABC中AC==．
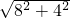分析：（1）连BD，通过角度代换和三角形的内角和定理求得∠BDE=90°即可．
（2）先得到BE，在△BDE中通过勾股定理可得到BD，再在△ABC中通过勾股定理求得AC．
点评：熟练掌握证明圆的切线方法，一般把证明圆的切线问题转化为证明线段垂直的问题．熟练利用勾股定理进行几何计算．