题目内容
已知△ABC中∠ACB=90°，CD⊥AB于D，∠A=30°，BC=2cm，则AD=
3cm
3cm
．分析：根据含30度角的直角三角形性质求出AB、BD，再相减即可．
解答：
解：∵△ABC中∠ACB=90°，∠A=30°，BC=2cm，
∴AB=2BC=4cm，∠B=60°，
∵DC⊥AB，
∴∠CDB=90°，
∴∠DCB=30°，
∴BD=
BC=1cm，
∴AD=AB-BD=4cm-1cm=3cm，
故答案为：3cm．
解：∵△ABC中∠ACB=90°，∠A=30°，BC=2cm，
∴AB=2BC=4cm，∠B=60°，
∵DC⊥AB，
∴∠CDB=90°，
∴∠DCB=30°，
∴BD=
| 1 |
| 2 |
∴AD=AB-BD=4cm-1cm=3cm，
故答案为：3cm．
点评：本题考查了含30度角的直角三角形性质的应用，注意：在直角三角形中，如果有一个角等于30度，那么它所对的直角边等于斜边的一半．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14、如图，已知△ABC中，AC+BC=24，AO、BO分别是角平分线，且MN∥BA，分别交AC于N、BC于M，则△CMN的周长为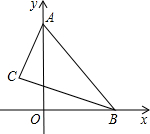
如图，已知△ABC中，AC=3，BC=4，直线AB的函数解析式是y=
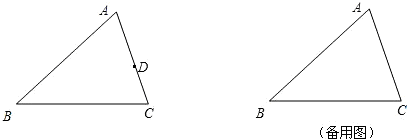意的△BMN唯一时，x的取值范围（请写出必要的解题过程）．
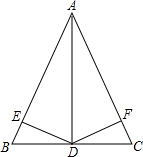如图，已知△ABC中，D是BC上一点，DE⊥AB，DF⊥AC，垂足分别为E、F．如果DE=DF，∠BAC=60°，AD=20cm，那么DE的长是