题目内容
 如图:已知Rt△ABC中∠C=90°,AC=3,BC=4,点E在AC上,E与A、C均不重合.
如图:已知Rt△ABC中∠C=90°,AC=3,BC=4,点E在AC上,E与A、C均不重合.(1)若点F在AB上,且EF平分△ABC的周长,设AE=x,用含x的代数式表示S△AEF;
(2)若点F在折线ABC上移动,是否存在直线EF将Rt△ABC的周长与面积同时平分?若存在,求出AE的长,若不存在,请说出理由.
分析:若求△AEF的面积,由已知知道其底边长,只需求出高就行了,利用平行线分线段成比例定理,建立中间量,即可求出其高度,第二问先假设成立,再建立平衡方程,进一步验证.最终得出结论.
解答:解:(1)过点F作FM⊥AC于M,
EF平分△ABC的周长,AE=x,所以可得AE+AF=CE+BC+BF,
即:x+AF=3-x+4+5-AF,解得AF=6-x.
由平行线分线段成比例定理可知,
AF:AB=FM:BC,即,6-x:5=FM:4,
解得FM=
,
所以S△AEF=
×
•x=
(2)若EF存在,
①当F在AB上时,如图1,
则由(1)可知,S△AEF=
=
×3×4×
=3,
化简得,2x2-12x+15=0,由△=122-4×2×15=24>0,
解得x1=
,x2=
(不合题意舍去).
即AE=
.
②当F在BC上时,如图2,
CF+CE=AE+AB+BF,
即CF+3-x=x+5+4-CF,
CF=3+
x,
根据面积平分得出S△CFE=S四边形BFEA=
S△ACB=3,
即
×(3-x)×(3+
x)=3,
解得:x3=
,x4=
(舍去),
即存在直线EF将Rt△ABC的周长与面积同时平分,AE的长是
或
.
EF平分△ABC的周长,AE=x,所以可得AE+AF=CE+BC+BF,
即:x+AF=3-x+4+5-AF,解得AF=6-x.
由平行线分线段成比例定理可知,
AF:AB=FM:BC,即,6-x:5=FM:4,
解得FM=
| 24-4x |
| 5 |
所以S△AEF=
| 1 |
| 2 |
| 24-4x |
| 5 |
| 12x-2 x2 |
| 5 |
(2)若EF存在,
①当F在AB上时,如图1,

则由(1)可知,S△AEF=
| 12-2x2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
化简得,2x2-12x+15=0,由△=122-4×2×15=24>0,
解得x1=
6-
| ||
| 2 |
6+
| ||
| 2 |
即AE=
6-
| ||
| 2 |
②当F在BC上时,如图2,

CF+CE=AE+AB+BF,
即CF+3-x=x+5+4-CF,
CF=3+
| 1 |
| 2 |
根据面积平分得出S△CFE=S四边形BFEA=
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
解得:x3=
-3+
| ||
| 2 |
-3-
| ||
| 2 |
即存在直线EF将Rt△ABC的周长与面积同时平分,AE的长是
6-
| ||
| 2 |
-3+
| ||
| 2 |
点评:能够将未知量通过求中间量建立等式关系,进而求解,另外对于类似第二问中的问题,可用假设的方法求解.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.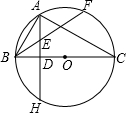 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF. 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P. 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为