题目内容
4.计算:(1)$\sqrt{24}$-$\sqrt{18}$×$\sqrt{\frac{1}{3}}$
(2)($\sqrt{24}$-$\sqrt{\frac{1}{2}}$)-($\sqrt{\frac{1}{8}}$+$\sqrt{6}$)
(3)$\frac{2}{b}$$\sqrt{a{b}^{5}}$•(-$\frac{3}{2}$$\sqrt{{a}^{3}b}$)÷3$\sqrt{\frac{b}{a}}$(a>0,b>0)
(4)$\sqrt{(-2)^{2}}$-$\sqrt{2}$($\sqrt{2}$-2)+$\frac{\sqrt{6}}{\sqrt{3}}$.
分析 (1)先进行二次根式的乘法运算,然后把$\sqrt{24}$化简后合并即可;
(2)先把各二次根式化为最简二次根式,然后去括号后合并即可;
(3)根据二次根式的乘除法则运算;
(4)根据二次根式的性质和乘除法则计算得到原式=2-2+2$\sqrt{2}$+$\sqrt{2}$,然后合并即可.
解答 解:(1)原式=2$\sqrt{6}$-$\sqrt{18×\frac{1}{3}}$=2$\sqrt{6}$-$\sqrt{6}$=$\sqrt{6}$;
(2)原式=2$\sqrt{6}$-$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{4}$-$\sqrt{6}$=$\sqrt{6}$-$\frac{3\sqrt{2}}{4}$;
(3)原式=$\frac{2}{b}$•(-$\frac{3}{2}$)•$\frac{1}{3}$•$\sqrt{a{b}^{5}•{a}^{3}b•\frac{a}{b}}$=-a2b$\sqrt{ab}$;
(4)原式=2-2+2$\sqrt{2}$+$\sqrt{2}$=3$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
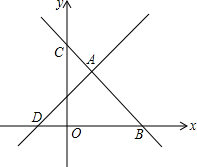 如图,已知直线y=-x+6与x轴交于点B,与y轴交于点C.直线y=x+2与直线y=-x+6交于点A,与x轴交于点D,点Q(3,t)在直线y=-x+6上.
如图,已知直线y=-x+6与x轴交于点B,与y轴交于点C.直线y=x+2与直线y=-x+6交于点A,与x轴交于点D,点Q(3,t)在直线y=-x+6上.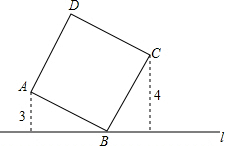 如图,直线l过正方形ABCD的顶点B,点A、点C到直线l的距离分别是3和4,则该正方形中AC的长是5$\sqrt{2}$.
如图,直线l过正方形ABCD的顶点B,点A、点C到直线l的距离分别是3和4,则该正方形中AC的长是5$\sqrt{2}$. 如图,点B、C在线段AD上,AC=DB,AF∥DE,AF=DE,求证:△ABF≌△DCE.
如图,点B、C在线段AD上,AC=DB,AF∥DE,AF=DE,求证:△ABF≌△DCE.