题目内容
14．在四边形中，如果任意的邻角都互补，则这个四边形一定是平行四边形．分析 由∠A+∠B=180°、∠A+∠D=180°利用“同旁内角互补，两直线平行”可得出AD∥BC、AB∥CD，再根据“两组对边分别平行的四边形为平行四边形”即可得出该四边形为平行四边形．
解答 解：依照题意画出图形，如图所示．
∵∠A+∠B=180°，∠A+∠D=180°，
∴AD∥BC，AB∥CD，
∴四边形ABCD为平行四边形．
故答案为：平行四边形．
点评 本题考查了多边形内角与外角、平行线的判定以及平行四边形的判定，根据“同旁内角互补，两直线平行”证出AD∥BC、AB∥CD是解题的关键．
练习册系列答案
相关题目
4．在△ABC中，∠A、∠B、∠C的对边长分别为a、b、c，且a2+c2=b2，则△ABC（ ）
| A． | ∠A为直角 | B． | ∠B为直角 | C． | ∠C为直角 | D． | 不是直角三角形 |
已知如图所示的Rt△ABC中，两直角边a、b满足a-b=1，斜边c=5，求△ABC的面积和周长．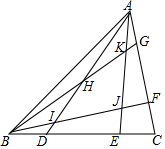
如图，在△ABC中，BC边上依次有B、D、E、C，AC边上依次有A、G、F，满足BD=CE=$\frac{1}{4}$BC，CF=AG=$\frac{1}{4}$AC，BF交AE于点J，交AD于I，BG交AE于点K，交AD于点H，且S△ABC=1，求S四边形KHIJ．