题目内容
5. 已知如图所示的Rt△ABC中,两直角边a、b满足a-b=1,斜边c=5,求△ABC的面积和周长.
已知如图所示的Rt△ABC中,两直角边a、b满足a-b=1,斜边c=5,求△ABC的面积和周长.
分析 先由勾股定理得:a2+b2=c2=25①,将a-b=1两边同时平方得:a2-2ab+b2=1②,两式可得:ab=12,可以求三角形ABC的面积,由a+b=$\sqrt{(a+b)^{2}}$可得a+b的值,可以计算三角形ABC的周长.
解答 解:由勾股定理得:a2+b2=c2=25①,
∵a-b=1,
∴a2-2ab+b2=1②,
把①代入②得:25-2ab=1,
ab=12,
∴S△ABC=$\frac{1}{2}$ab=$\frac{1}{2}$×12=6,
∵a+b=$\sqrt{(a+b)^{2}}$=$\sqrt{{a}^{2}+2ab+{b}^{2}}$=$\sqrt{25+2×12}$=7,
∴△ABC的周长=7+5=12.
点评 本题考查了完全平方公式、勾股定理的证明和运用、三角形面积,熟练掌握利用面积法证明勾股定理,本题难度适中.

练习册系列答案
相关题目
16.某生姜种植基地计划种植A、B两种生姜30亩,已知A、B两种生姜的年产量分别为2000千克/亩、2500千克/亩.若该基地收获A、B两种生姜的年总产量为68000千克,求A、B两种生姜各种多少亩?
17.下列长度的三条线段能组成钝角三角形的是( )
| A. | 3,4,4 | B. | 3,4,5 | C. | 3,4,7 | D. | 3,4,6 |
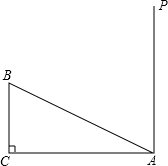 如图,有一个Rt△ABC,∠C=90°,AC=16,BC=8,一条线段MN=AB,M、N分别在AC和过点A且垂直于AC的射线AP上运动,问:点M运动到什么位置,才能使△ABC和△ANM全等.
如图,有一个Rt△ABC,∠C=90°,AC=16,BC=8,一条线段MN=AB,M、N分别在AC和过点A且垂直于AC的射线AP上运动,问:点M运动到什么位置,才能使△ABC和△ANM全等.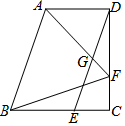 如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD,点E,F分别在边BC,CD上,
如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD,点E,F分别在边BC,CD上,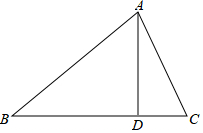 如图,D为△ABC边BC上的一点,AB=20,AC=13,AD=12,DC=5,则S△ABC=126.
如图,D为△ABC边BC上的一点,AB=20,AC=13,AD=12,DC=5,则S△ABC=126.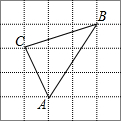 图中的小正方形边长为1,△ABC的三个顶点都在小正方形的顶点上,求:
图中的小正方形边长为1,△ABC的三个顶点都在小正方形的顶点上,求:


