Question

13．如图，矩形ABCD中，BC=10，∠BAC=30°，若在AC、AB上各取一点M、N，使BM+MN的值最小，求这个最小值15．

Answer 1

分析 作点B关于AC的对称点B′，由轴对称图形的性质可知：BM=B′M，AB=AB′，∠BAC=∠B′AC=30°，从而可知△BAB′为等边三角形，过点B′作B′N⊥AB，交AC于点M，则MB+MN=B′N，然后依据特殊锐角三角函数可求得B′N的长．

解答 解：如图所示：作点B关于AC的对称点B′，过点B′作B′N⊥AB，交AC于点M．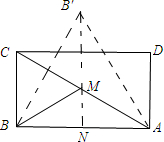

∵在Rt△ABC中，∠BAC=30°，
∴AB=$\sqrt{3}$BC=10$\sqrt{3}$．
∵点B与点B′关于AC对称，
∴AB=AB′，∠BAC=∠B′AC=30°．
∴∠BAB′=60°．
∴△BAB′是等边三角形．
∵B′N⊥AB，
∴B′N=BB′×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}×\frac{\sqrt{3}}{2}$=15．
∵点B与点B′关于AC对称，
∴BM=B′M．
∴BM+MN=B′M+MN=B′N=15．
故答案为：15．

点评 本题主要考查的是轴对称-路径最短问题，解答本题需要同学们熟练掌握轴对称图形的性质、等边三角形的性质和判定、特殊锐角三角三角函数值，证得△BAB′是等边三角形是解题的关键．