题目内容
12.已知抛物线C1:y=$\frac{5}{9}$(x+2)2-5的顶点为P,与x轴相交于A、B两点(点A在点B的左边),将抛物线沿x轴翻折,再向右平移t个单位,平移后的抛物线C2的顶点为M,直接写出当t=0和t=2时抛物线C2的解析式.分析 因为将抛物线沿x轴翻折,所以得到的新抛物线和原抛物线关于x轴对称,进而可求出新抛物线的解析式,再根据抛物线平移的性质即可求出当t=0和t=2时抛物线C2的解析式.
解答 解:∵抛物线C1:y=$\frac{5}{9}$(x+2)2-5,
∴将抛物线沿x轴翻折后的抛物线解析式为-y=$\frac{5}{9}$(x+2)2-5,
即y=-$\frac{5}{9}$(x+2)2+5,
∴当t=0时抛物线C2的解析式为:y=-$\frac{5}{9}$(x+2)2+5,
当t=2时抛物线C2的解析式为:y=-$\frac{5}{9}$x2+5.
点评 本题考查了二次函数图象与几何变换,此类题目利用定点的变换确定解析式的变化更简便,难点在于确定出平移后的抛物线的顶点坐标.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
4.求一个数的立方根,有些数可以直接求得,如$\root{3}{8}$,有些数则不能直接求得,如$\root{3}{5}$,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
(1)表中所给的信息中,你能发现什么规律?(请将规律用文字表达出来)
(2)运用你发现的规律,探究下列问题:
已知$\root{3}{2.5}$≈1.36,求下列各数的立方根:
①0.0025; ②2500000.
| n | 8 | 0.008 | 0.000008 | 8000 | 8000000 | … |
| $\root{3}{n}$ | 2 | 0.2 | 0.02 | 20 | 200 | … |
(2)运用你发现的规律,探究下列问题:
已知$\root{3}{2.5}$≈1.36,求下列各数的立方根:
①0.0025; ②2500000.
19.在数-27,-1.25,0,$\frac{24}{7}$中,立方根为正数的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
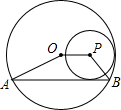 如图,⊙P内切于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP,若⊙O的半径为3,⊙P的半径为1,则四边形ABPO的面积为2$+2\sqrt{2}$.
如图,⊙P内切于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP,若⊙O的半径为3,⊙P的半径为1,则四边形ABPO的面积为2$+2\sqrt{2}$.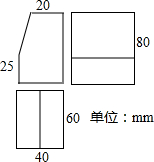 已知一个几何体的三视图如图所示.
已知一个几何体的三视图如图所示.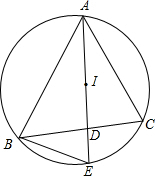 如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆于点E.
如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆于点E.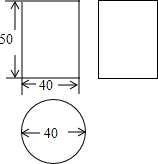 某工厂接受了加工100件密封罐的任务,设计者给出了密封罐的三视图(如图所示,单位:cm),已知加工这种密封罐需全部用铁皮焊接,那么该工厂至少要准备多少平方米的铁皮?
某工厂接受了加工100件密封罐的任务,设计者给出了密封罐的三视图(如图所示,单位:cm),已知加工这种密封罐需全部用铁皮焊接,那么该工厂至少要准备多少平方米的铁皮?